فهرست مطالب
Toggleتوابع مثلثاتی ازجمله مباحث کاربردی برای درک برخی از مسائل در دنیای واقعی هستند. اگر بهیاد داشته باشید، ما در آموزشهای پیشین توابع دیگر مثلثاتی ازجمله سینوس، کسینوس و تانژانت را معرفی کردیم. اکنون نوبت معرفی تابع مثلثاتی دیگری بهنام تابع کتانژانت است.
کتانژانت مانند سایر توابع مثلثاتی دارای ویژگیهای خاصی است که در این مقاله با آنها آشنا خواهیم شد. اگر مایل هستید بدانید تابع کتانژانت چیست و کتانژانت یک زاویه چگونه محاسبه میشود، پیشنهاد میکنیم این مطلب از مدرسه سلام را تا انتها مطالعه کنید.
کتانژانت چیست ؟
تابع «کتانژانت» (Cotangent) را بهاختصار بهصورت cot نشان میدهند. درست مانند سایر نسبتهای مثلثاتی، فرمول کتانژانت نیز بهصورت
نسبت اضلاع یک مثلث قائم الزاویه تعریف میشود. اگر یک مثلث قائمالزاویه مانند شکل زیر داشته باشیم که زاویه بین یکی از ساقهای آن و وتر، زاویه حاده θ باشد، در این صورت، کتانژانت زاویه θ از نسبت ضلع مجاور این زاویه به ضلع مقابل آن بهدست میآید. دقت داشته باشید که ضلع مجاور ضلعی غیر از وتر مثلث است.

با توجه به این تعریف، تابع کتانژانت را میتوانیم برحسب سینوس و کسینوس نیز بنویسیم:
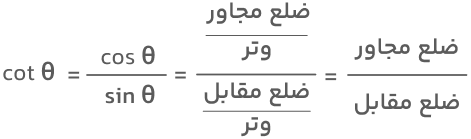
این نسبت دقیقاً عکس نسبت تعریفشده در تابع تانژانت است؛ بدین معنا که حاصلضرب تانژانت یک زاویه در کتانژانت آن زاویه مساوی با یک است.
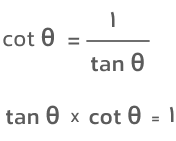

اولین نفری باشید که از اخبار و اطلاعیههای مرتبط با پایه تحصیلیتان باخبر میشود!
کتانژانت در دایره مثلثاتی
منظور از دایره مثلثاتی دایرهای به شعاع ۱ است که مرکز آن در مبدأ مختصات قرار دارد. اگر از نقطه (۱,۰) روی محیط دایره شروع به دوران کنیم و یک دور کامل در خلاف جهت عقربههای ساعت بزنیم تا مجدد به نقطه شروع بازگردیم، بهاندازه ۲π رادیان یا ۳۶۰ درجه طی کردهایم.
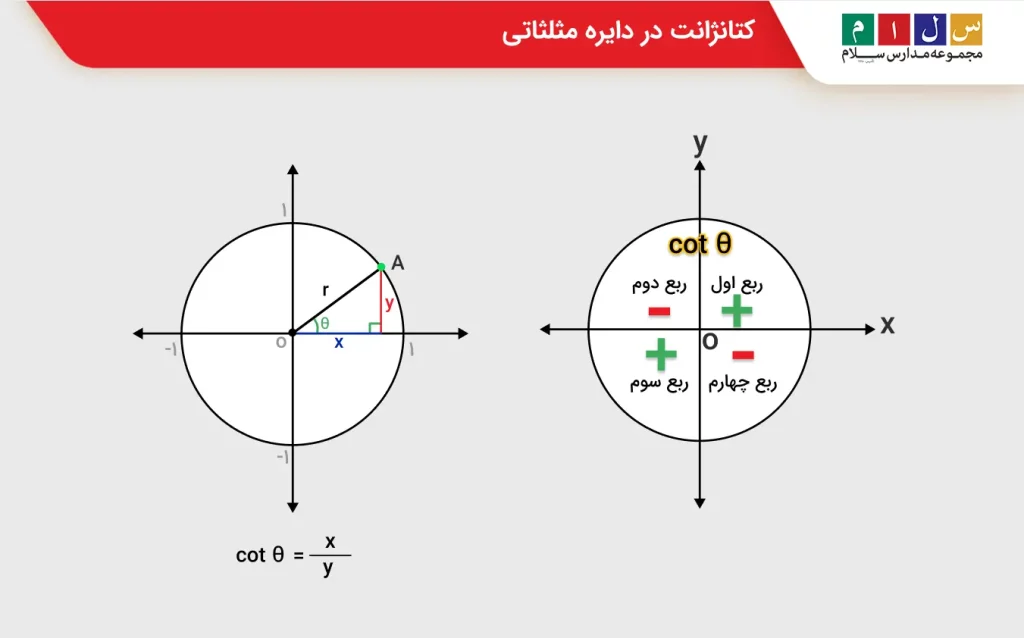
نقطهای مثل A با مختصات (x,y) را روی محیط دایره در نظر بگیرید. این نقطه را به مبدأ مختصات که مرکز دایره است وصل میکنیم و زاویهای که این خط با محور xها میسازد را θ مینامیم. در این صورت کتانژانت زاویه برابر است با:
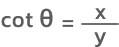
طبق این رابطه، مقدار کتانژانت در ربع اول و سوم مثبت و در ربع دوم و چهارم منفی است زیرا در ربع اول و سوم مقادیر x و y همعلامتاند اما در ربع دوم و چهارم علامتشان با هم فرق میکند.
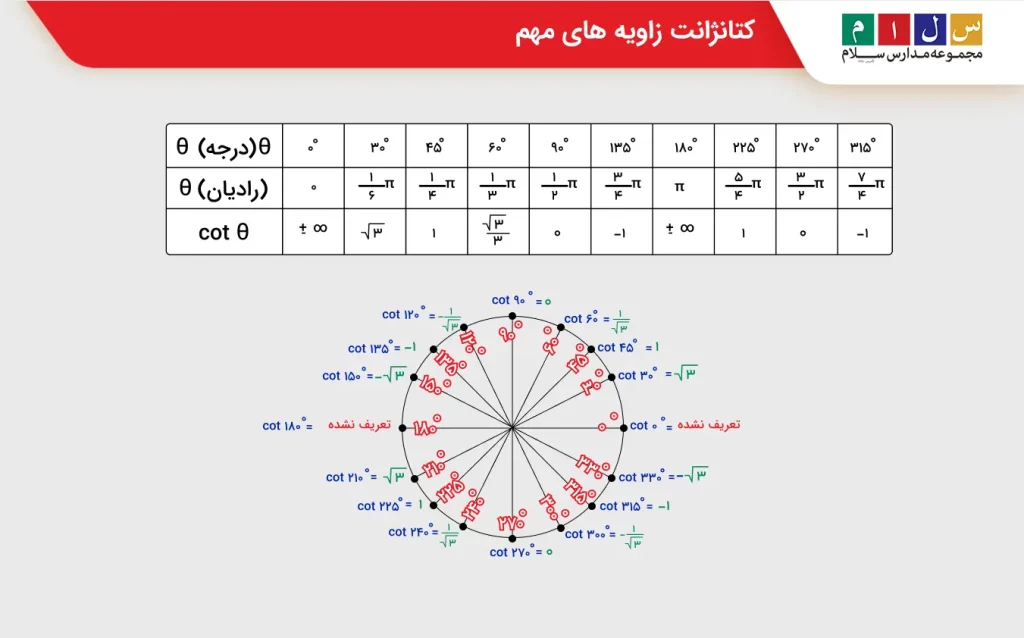
جدول کتانژانت زاویه های پرکاربرد
اکنون که با تابع سینوس و کسینوس آشنا هستیم و میدانیم کتانژانت زاویه بهصورت نسبت کسینوس به سینوس آن زاویه تعریف میشود، میتوانیم مقادیر کتانژانت زوایای مهم را بهدست آوریم. برای دسترسی راحتتر به این مقادیر، کتانژانت زاویههای مختلف را در یک جدول نوشتهایم و روی دایره مثلثاتی نیز نشان دادهایم.
محاسبه کتانژانت ۳۰ درجه
برای مشخص کردن درستی مقدار کتانژانت ۳۰ درجه در جدول بالا کافیست از نسبت کسینوس ۳۰ درجه به سینوس ۳۰ درجه استفاده کنیم. ازآنجا که مقدار کسینوس ۳۰ درجه برابر با و مقدار سینوس ۳۰ درجه مساوی با
است مقدار کتانژانت این زاویه بهصورت زیر بهدست خواهد آمد:
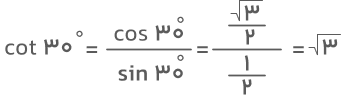
محاسبه کتانژانت ۱۸۰ درجه
کتانژانت ۱۸۰ درجه را از تقسیم مقدار کسینوس این زاویه به مقدار سینوس آن بهدست میآوریم. مقدار کسینوس و سینوس ۱۸۰ درجه را میدانیم. کافیست مقادیر را جایگذاری کنیم.

بهاینترتیب، میتوانیم مقدار کتانژانت سایر زوایا را نیز تعیین کنیم و صحت مقادیری را که در جدول آوردهایم بسنجیم.
نمودار کتانژانت
اگر به مقادیر تابع کتانژانت با زاویههای مختلف نگاه کنید متوجه خواهید شد که این تابع مثلثاتی در ۰ و ۱۸۰ درجه تعریفنشده است و از ۰ تا ۱۸۰ درجه و از ۱۸۰ تا ۳۶۰ درجه مقادیرش تکرار میشود. این بدین معناست که تابع کتانژانت یک تابع متناوب است و شکل نمودار آن در هر دوره تناوب تکرار میشود.
رسم تابع کتانژانت
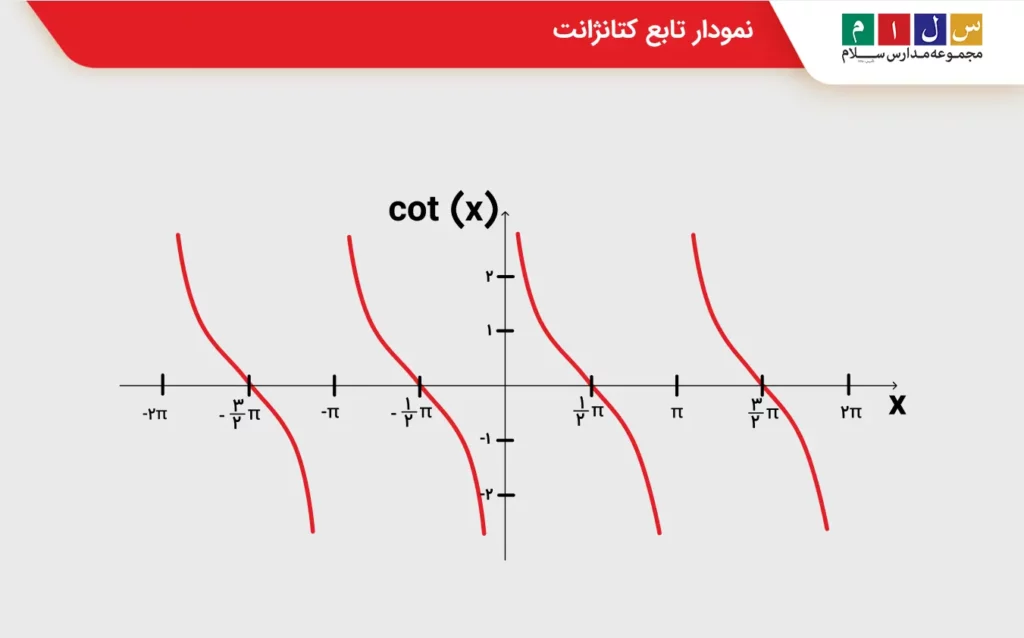
حالا که مقادیر کتانژانت زوایای پرکاربرد را داریم، رسم تابع کتانژانت آسان خواهد بود. برای رسم این تابع، ابتدا دو محور x و y را رسم میکنیم. محور xها را مقدار زاویه برحسب رادیان و محور yها را محور کتانژانت در نظر میگیریم. همانطور که گفتیم، مقدار کتانژانت در زوایایی که مضرب صحیحی از π هستند، بینهایت یا تعریفنشده است. پس این زاویهها مجانبهای قائم تابع کتانژانت به شمار میروند.
ازطرفی، در فواصل π رادیان، مقادیر تابع تناوبی است و نمودار آن از یک الگو پیروی میکند. برای اینکه نمودار کتانژانت را دقیقتر رسم کنیم، در محور xها بهجای π عدد پی یعنی ۳/۱۴ را قرار میدهیم. برای اینکه شکل نمودار مشخص شود، چند نقطه دلخواه را معین کرده و به هم وصل میکنیم. درنهایت، نموداری به شکل زیر خواهیم داشت که تکراری بودن آن در فواصل π کاملاً مشهود است.
ویژگی های کتانژانت چیست ؟
تابع کتانژانت خصوصیاتی دارد که آگاهی از آنها برای درک بهتر و حل راحتتر مسئلههای مثلثاتی حائز اهمیت است. این خصوصیات عبارتاند از:
- کتانژانت تابعی فرد است. منظور از فرد بودن این تابع این است که اگر در فرمول کتانژانت بهجای یک زاویه، قرینه آن را قرار دهیم، مقدار کتانژانت قرینه زاویه برابر با منفی مقدار کتانژانت زاویه اولیه خواهد بود. این ویژگی بهصورت زیر اثبات میشود:
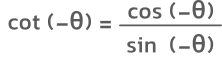
با توجه به فرد بودن تابع سینوس و زوج بودن تابع کسینوس داریم:

- کتانژانت یک تابع متناوب است. همانگونه که قبلاً هم اشاره کردیم، دوره تناوب تابع کتانژانت π است.

در اینجا n یک عدد صحیح است.
- دامنه تابع کتانژانت تمام اعداد حقیقی بهجز مضربهای صحیح π و برد آن تمام اعداد حقیقی است. دلیل اینکه مضربهای صحیح π در دامنه تابع کتانژانت قرار ندارد این است که مقادیر تابع در این زوایا تعریفنشده است.
فرمول کتانژانت چیست ؟
در اینجا چند فرمول مهم کتانژانت را معرفی میکنیم. این فرمولها از توابع مثلثاتی دیگر حاصل میشوند.
- فرمول کتانژانت جمع دو زاویه
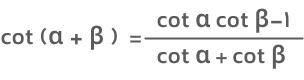
- فرمول کتانژانت تفریق دو زاویه
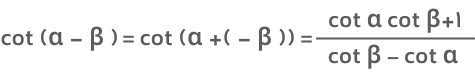
- فرمول کتانژانت دو برابر زاویه
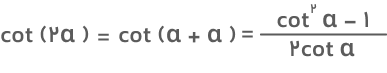
- فرمول کتانژانت نصف زاویه
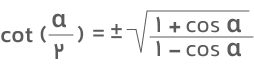
- فرمول کتانژانت برحسب سینوس
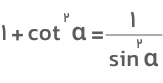
پیشنهاد مطالعه: سینوس چیست؟
مثال های تابع کتانژانت
مثال ۱: کتانژانت ۷۵ درجه را تعیین کنید.
جواب: زاویه ۷۵ درجه از مجموع زوایای ۳۰ و ۴۵ درجه بهدست میآید. پس میتوانیم با استفاده از فرمول کتانژانت جمع دو زاویه و همچنین مقدار کتانژانت ۳۰ و ۴۵ درجه کتانژانت این زاویه را محاسبه کنیم. خواهیم داشت:
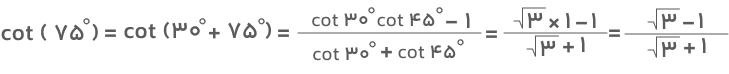

جواب: در این سؤال میتوانیم از خاصیت تناوبی بودن تابع کتانژانت استفاده کنیم و آن را بهصورت زیر بنویسیم:

مثال ۳: درستی رابطه زیر را اثبات کنید.
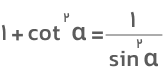
جواب: برای اثبات کافیست نسبت کسینوس به سینوس را بهجای کتانژانت قرار دهیم تا به طرف راست تساوی برسیم:
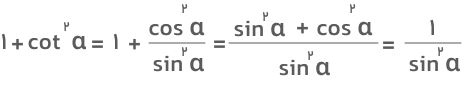
سخن پایانی
در این مقاله آموختیم که کتانژانت چیست و چگونه محاسبه میشود. کتانژانت یکی از شش تابع اصلی مثلثاتی است که در علوم مختلف کاربرد دارد. این تابع ویژگیهایی دارد که آشنایی با آنها برای درک بهتر مثلثات کمککننده خواهد بود. همچنین فرمولهای مهمی که برای این تابع معرفی کردیم، در اثبات فرمولهای مثلثاتی و محاسبه زاویههای گوناگون به کارتان خواهد آمد. امیدواریم با خواندن این مقاله پاسخ سؤالهای خود را دریافت کرده باشید.
سؤالات متداول
- فرمول کتانژانت چیست ؟
کتانژانت یک زاویه از تقسیم مقدار کسینوس آن زاویه بر مقدار سینوس بهدست میآید. در مثلث قائمالزاویه فرمول کتانژانت زاویه بهصورت نسبت ضلع مجاور آن زاویه به ضلع مقابلش تعریف میشود. - دامنه و برد تابع کتانژانت چیست ؟
دامنه تابع کتانژانت شامل تمام اعداد حقیقی غیر از مضربهای صحیح π است و برد آن نیز تمام اعداد حقیقی را شامل میشود. - تابع کتانژانت زوج است یا فرد؟
کتانژانت یک تابع فرد است. - کتانژانت ۳۰ درجه چند است؟
کتانژانت ۳۰ درجه برابر است با ۳√. - کتانژانت ۱۸۰ درجه چند است؟
کتانژانت این زاویه تعریفنشده است. - کتانژانت ۴۵ درجه چقدر است؟
کتانژانت ۴۵ درجه مساوی با ۱ است.









