تانژانت در مثلثات چیست؟ ׀ ویژگی ها + جدول تانژانت زاویه ها

تابع تانژانت یکی از شش تابع اصلی مثلثاتی است که کاملاً پرکاربرد محسوب می‌‌شود. این تابع مثلثاتی از نسبت تابع سینوس به تابع کسینوس به‌‌دست می‌‌آید و مانند سایر توابع مثلثاتی بیشتر جنبه هندسی دارد، اما در بسیاری از محاسبات مربوط به سایر علوم نیز به‌‌کار می‌‌رود.

در این مجموعه از آموزش‌‌های درس ریاضی قصد داریم به تابع تانژانت بپردازیم و ویژگی‌‌های آن ازجمله دامنه و برد، زوج یا فرد بودن و غیره را بررسی کنیم. همچنین در کنار نمودار و فرمول‌‌های این تابع، برای فهم بهتر چند مثال نیز حل خواهیم کرد.

تعریف تانژانت

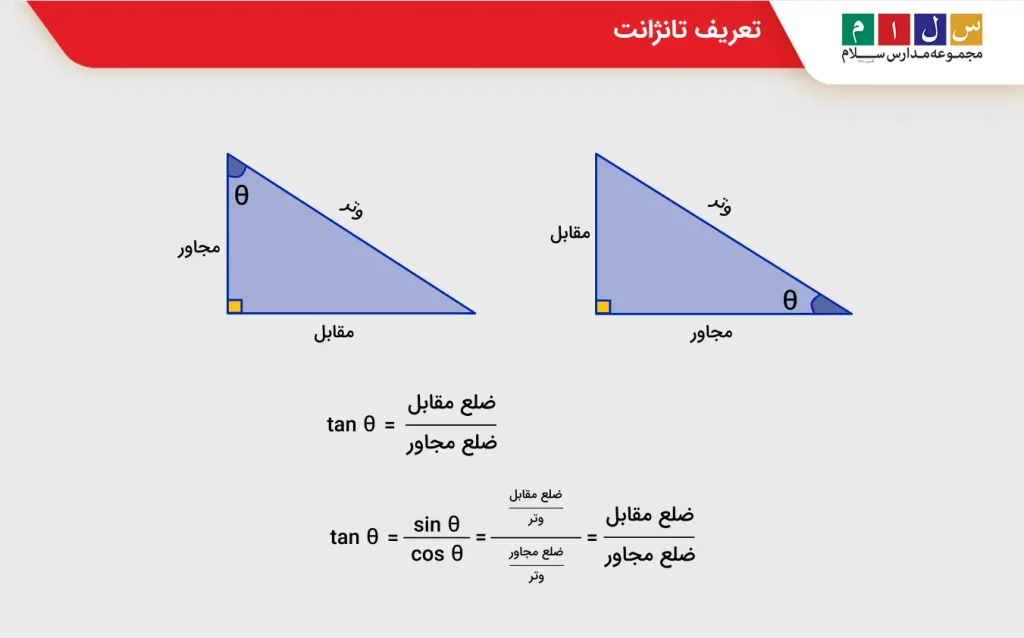
«تانژانت» (Tangent) یک تابع مثلثاتی است که می‌‌توان آن را با کمک یک مثلث قائم‌‌ الزاویه تعریف کرد. همان‌‌طور که در مقاله کسینوس چیست و سینوس ریاضی دهم نیز خواندیم، در تعریف توابع مثلثاتی از یک مثلث قائم‌‌الزاویه استفاده می‌‌شود. فرض کنید مثلثی با یک زاویه قائمه داریم. در این نوع مثلث، دو زاویه‌‌ای که قائمه نیستند، همواره اندازه‌‌ای کمتر از ۹۰ درجه دارند یا به‌‌عبارتی زاویه حاده هستند.

اگر یکی از این زاویه‌‌های حاده را θ در نظر بگیریم، آنگاه ضلعی را که روبه‌‌روی این زاویه قرار دارد، ضلع مقابل و ضلعی را که در کنار زاویه وجود دارد و وتر نیست، ضلع مجاور می‌‌نامند. با توجه به این نام‌‌گذاری، تابع تانژانت به‌‌صورت زیر بیان خواهد شد:

اگر دقت کنید، از نسبت تابع سینوس به تابع کسینوس نیز می‌‌توان به این رابطه رسید:

پس فرمول دیگر تانژانت را می‌‌توان به‌‌صورت زیر نوشت:

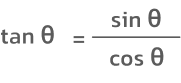
مثال ۱: در شکل زیر، تانژانت زاویه θ را به‌‌دست آورید.

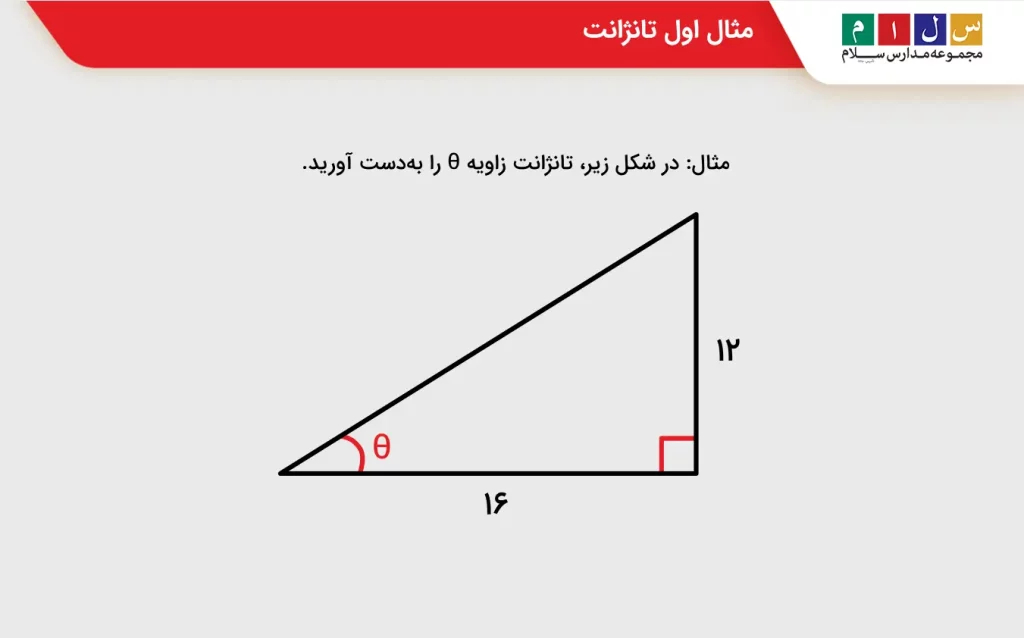
جواب: برای محاسبه تانژانت θ از فرمولی که معرفی کردیم کمک می‌‌گیریم و مقادیر معلوم را در آن جای‌‌گذاری می‌‌کنیم. داریم:

مثال ۲: در تصویر زیر فردی را مشاهده می‌‌کنید که در فاصله ۱۷متری از پایه یک درخت ایستاده است. با توجه به اینکه زاویه بین پاهای فرد و بالای درخت ۴۹ درجه است، ارتفاع درخت چند متر خواهد بود؟ اگر درخت به‌‌سمت این شخص بیفتد، آیا روی او فرود خواهد آمد؟

جواب: شکل بالا یک مثلث قائم‌‌الزاویه است. پس برای تعیین ارتفاع درخت که ضلع مقابل زاویه است، می‌‌توانیم از تعریف تانژانت استفاده کنیم:

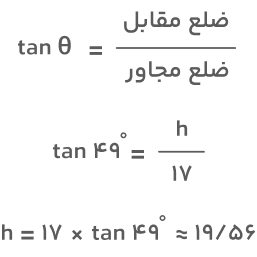
بنابراین، ارتفاع درخت تقریباً ۱۹/۵۶ متر است. ازآنجا که ۱۹/۵۶>۱۷ است، اگر درخت در جهتی که شخص ایستاده است بیفتد روی او فرود خواهد آمد.

تانژانت در دایره مثلثاتی

دایره مثلثاتی دایره‌‌ای با مرکز مبدأ مختصات و شعاع واحد یعنی ۱ است. اگر از یک نقطه روی محیط این دایره شروع کنیم و یک دور کامل بچرخیم تا دوباره به همان نقطه برسیم، مسافتی به‌‌اندازه ۳۶۰ درجه یا ۲π رادیان طی خواهیم کرد. اگر مانند تصویر زیر، نقطه‌‌ای دلخواه مانند A با مختصات(x,y) روی محیط دایره در نظر بگیریم و آن را به مرکز دایره که مبدأ مختصات است وصل کنیم، نقطه A زاویه‌‌ای را نشان خواهد داد که تانژانت آن از رابطه زیر تعیین می‌‌شود:

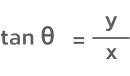
دایره مثلثاتی شامل ۴ ناحیه است که آن‌‌ها را ربع اول، دوم، سوم و چهارم می‌‌نامیم. با توجه به نسبت معرفی‌‌شده برای تانژانت و با توجه به اینکه مقادیر x و y در ربع اول و سوم هم‌‌علامت و در ربع دوم و چهارم غیرهم‌‌علامت‌‌اند، می‌‌توان به این نتیجه رسید که مقدار این تابع مثلثاتی در ربع اول و سوم مثبت و در ربع دوم و چهارم منفی است.

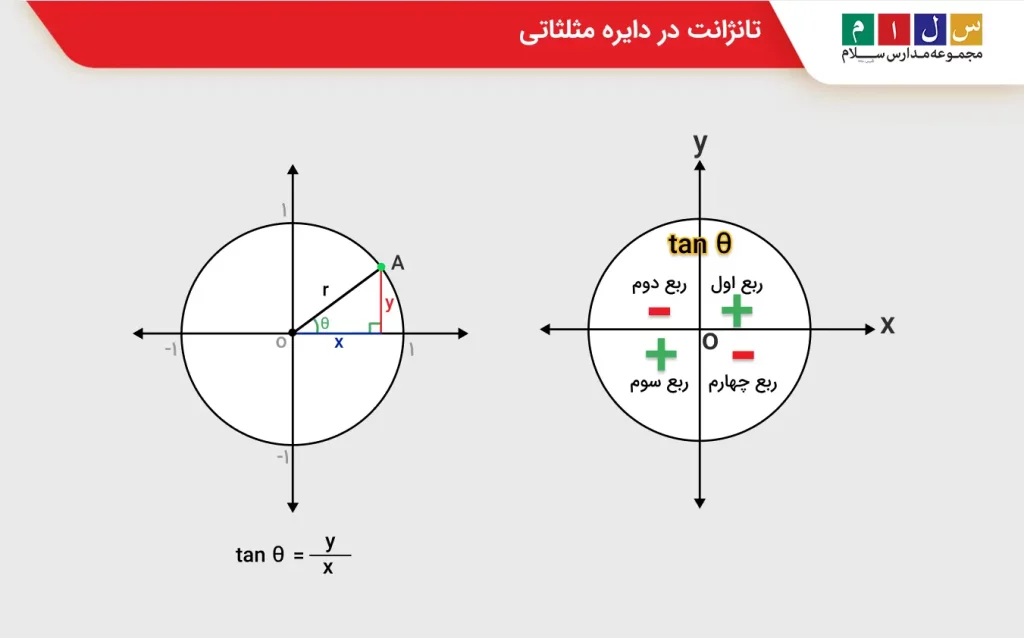
جدول تانژانت تمام زاویه ها

در حل بسیاری از مسائل مثلثاتی دانستن و به خاطر سپردن مقدار تانژانت برخی از زوایا کمک‌‌کننده است. به همین منظور، ما در اینجا جدول تانژانت زاویه های پرکاربرد را در اختیارتان قرار خواهیم داد.

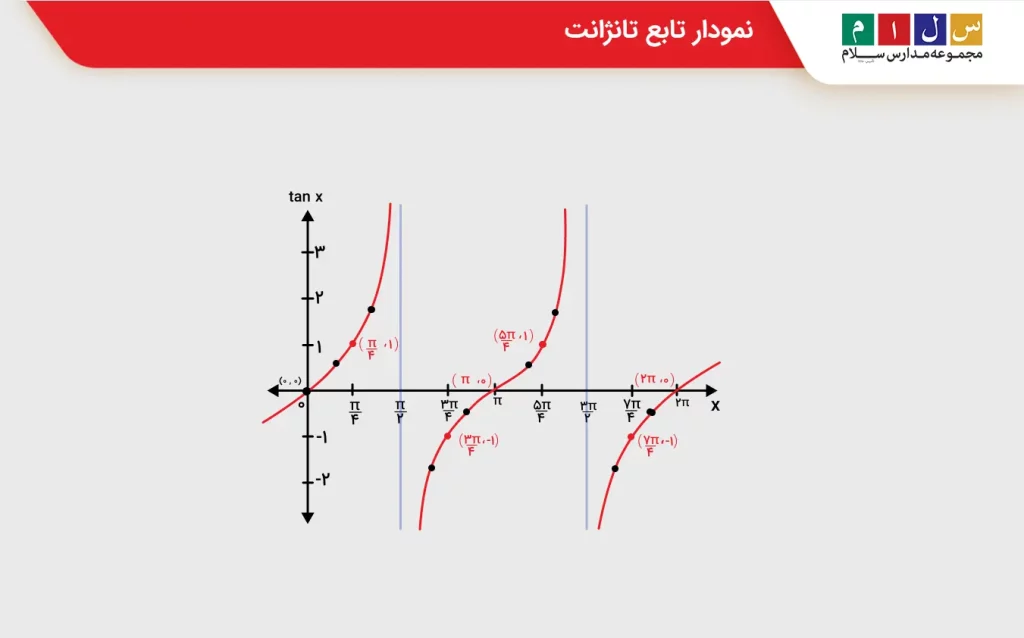
رسم تابع تانژانت

برای رسم تابع تانژانت از مقادیر جدولی که در بخش قبل ارائه کردیم می‌‌توانیم استفاده کنیم. برای این کار کافی‌‌ست محور xها را اندازه زاویه برحسب رادیان و محور yها را مقدار تانژانت قرار دهیم. با توجه به جدول، زاویه‌‌هایی که مضرب فردی از هستند، به‌‌عنوان مجانب قائم در نظر گرفته می‌‌شوند زیرا در این زاویه‌‌ها مقدار تانژانت بی‌‌نهایت یا تعریف‌‌نشده است.

برای رسم نمودار، ابتدا مانند تصویر زیر چند نقطه را مشخص می‌‌کنیم و سپس با وصل کردن آن‌‌ها شکل کلی نمودار تابع را به‌‌دست می‌‌آوریم. هنگام مشخص کردن نقاط، می‌‌توانیم از تقریب مقادیر به‌‌صورت زیر استفاده کنیم:

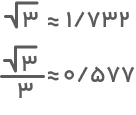
همچنین برای رسم دقیق‌‌تر نمودار، مقادیر روی محور افقی را با جای‌‌گذاری عدد ۳/۱۴ به‌‌جای π به‌‌دست می‌‌آوریم. نمودار تانژانت نشان می‌‌دهد که این تابع مثلثاتی متناوب بوده و دوره تناوب آن نیز π است؛ یعنی نمودار در فواصل π رادیان تکرار می‌‌شود.

پیشنهاد مطالعه : کتانژانت چیست

ویژگی های تابع تانژانت

تابع تانژانت مانند سایر توابع مثلثاتی خصوصیاتی دارد که به شرح زیر است:

• تانژانت یک تابع فرد است. این ویژگی را با قرینه کردن مقدار زاویه در فرمول تانژانت می‌‌توان به‌‌شکل زیر اثبات کرد:

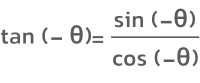
می‌‌دانیم که سینوس تابعی فرد و کسینوس تابعی زوج است. پس خواهیم داشت:

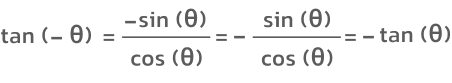
• تابع تانژانت تابعی متناوب است. دوره تناوب این تابع مثلثاتی برابر است با π.

n یک عدد صحیح است. مثال‌‌های زیر نمونه‌‌هایی از خاصیت تناوب تابع تانژانت هستند.

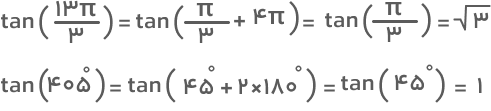
دامنه تابع تانژانت تمام اعداد حقیقی به‌‌جز مضرب‌‌های فرد و برد آن تمام اعداد حقیقی است. اگر به یاد داشته باشید در بخش رسم تابع تانژانت توضیح دادیم که در مضرب‌‌های فرد تابع تانژانت تعریف‌‌نشده (بی‌‌نهایت) است. به همین دلیل نمی‌‌توانیم این مقادیر را جزئی از دامنه در نظر بگیریم.

پیشنهاد مطالعه: عدد پی(π)چیست ؟

فرمول تانژانت

در این بخش چند فرمول معروف تابع تانژانت را که با استفاده از تعریف سایر توابع مثلثاتی به‌‌دست می‌‌آیند معرفی می‌‌کنیم.

• فرمول تانژانت مجموع دو زاویه

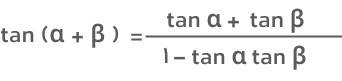
• فرمول تانژانت تفاضل دو زاویه

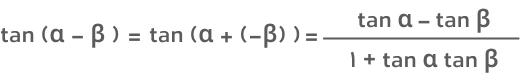
• فرمول تانژانت دو برابر زاویه

• فرمول تانژانت نصف زاویه

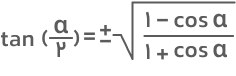
علامت مثبت و منفی در این فرمول بستگی به ناحیه‌‌ای دارد که زاویه در آن واقع شده است.

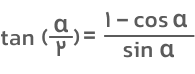
مثال ۱: تانژانت ۱۵ درجه را محاسبه کنید.
جواب: زاویه ۱۵ درجه نصف ۳۰ درجه است. بنابراین برای تعیین مقدار تانژانت آن کافی‌‌ست از فرمول تانژانت نصف زاویه استفاده کنیم. داریم:

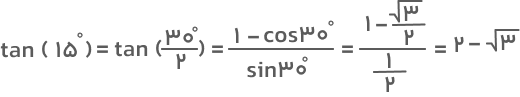
این مثال را می‌‌توان با فرمول‌‌های دیگری نیز حل کرد. به‌‌عنوان تمرین می‌‌توانید از سایر فرمول‌‌ها استفاده کنید و با جواب به‌‌دست‌‌آمده آن را مقایسه کنید.

مثال ۲: درستی تساوی زیر را ثابت کنید.

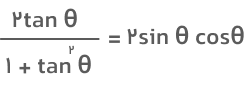
جواب: برای رسیدن به عبارت سمت راست تساوی، لازم است ابتدا tan را برحسب sin و cos بنویسیم و اندکی ساده‌‌سازی انجام دهیم.

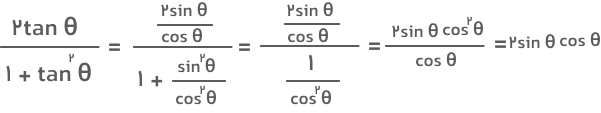
سخن پایانی

در این مطلب یاد گرفتیم که تابع تانژانت از نسبت تابع سینوس به کسینوس به‌‌دست می‌‌آید. ازجمله مهم‌‌ترین ویژگی‌‌های این تابع می‌‌توان به متناوب و فرد بودن آن اشاره کرد که در حل مسائل مربوط به مثلثات بسیار به‌‌کار می‌‌آیند. برای این تابع مثلثاتی چند فرمول مهم و کاربردی ازقبیل فرمول تانژانت جمع دو زاویه و تفریق دو زاویه نیز معرفی کردیم تا در اثبات تساوی‌‌ها و حل مسائل بتوانید از آن‌‌ها استفاده کنید.

طبق توضیحاتی که داده شد، مقدار تانژانت در دایره مثلثاتی پس از طی شدن هر π رادیان تکرار می‌‌شود و از همین روست که این تابع را یک تابع تناوبی به شمار می‌‌آورند. به‌‌عنوان یک جمع‌‌بندی، در ادامه به چند سؤال رایج که احتمالاً سؤال شما نیز باشد پاسخ می‌‌دهیم.

سؤالات متداول

1. تانژانت چه زاویه ای منفی یک است ؟
   تانژانت زاویه‌‌های مساوی با منفی یک است.
2. تانژانت زاویه ۴۵ درجه چند است ؟
   تانژانت ۴۵ درجه مساوی ۱ است.
3. تانژانت چه زاویه ای ۲ است ؟
   با استفاده از وارون تابع تانژانت و با کمک ماشین‌‌حساب می‌‌توان این زاویه را تعیین کرد. این زاویه تقریباً ۶۳/۴۳ درجه است. همچنین به‌‌دلیل اینکه دوره تناوب تانژانت π رادیان است( tan ( nπ+۶۳/۴۳ برابر ۲ خواهد بود.
4. تانژانت چه زاویه ای برابر ۵ است ؟
   با ماشین‌‌حساب مقدار تقریبی این زاویه ۷۸/۶۹ درجه به‌‌دست می‌‌آید. با توجه به متناوب بودن تابع تانژانت، تمام زاویه‌‌های nπ+۷۸/۶۹ را می‌‌توان به‌‌عنوان جواب در نظر گرفت.
5. تانژانت ۱۸۰ درجه چند است؟
   مقدار تانژانت این زاویه صفر است.
6. تانژانت ۹۰ درجه چقدر است؟
   تانژانت ۹۰ درجه تعریف‌‌نشده (بی‌‌نهایت) است.