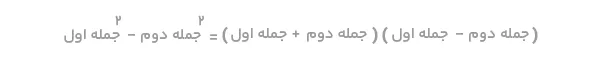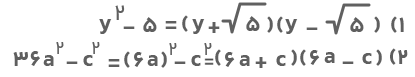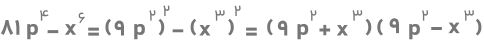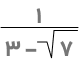فهرست مطالب
Toggleاتحادها نقش بسیار مهمی در ساده کردن عبارتها و حل مسائل جبری و مثلثاتی دارند. بنابراین، اهمیت یادگیری آنها برای پایههای بالاتر را نمیتوان انکار کرد. شیوه صحیح آموزش و حل نمونه سؤالهای متعدد و کاربردی نقش تعیینکنندهای در یادگیری اتحادها ایفا میکنند و قطعاً عامل مهمی در جذاب کردن فهم آنها برای دانشآموزان خواهند بود.
اگر دانشآموز پایه نهم هستید و میخواهید با اتحاد مزدوج که یکی از اتحادهای معروف در ریاضی است آشنا شوید، جای درستی آمدهاید. در این مقاله قرار است اتحاد مزدوج را از صفر تا صد آموزش ببینید. ابتدا با اتحاد مزدوج آشنا میشوید و سپس، اثبات فرمول آن را بهصورت جبری و هندسی یاد میگیرید. در پایان نیز با استفاده از مثالهای حلشدهای که آورده شده است روش تجزیه و کاربرد این اتحاد را بهطور کامل میآموزید.
اتحاد مزدوج چیست؟
اتحاد مزدوج که به آن «تفاضل دو مربع» نیز گفته میشود، بیان میکند که تفاضل مربع دو عدد یا دو جمله برابر است با حاصلضرب مجموع دو عدد یا دو جمله در تفاضل آنها.
طبق این تعریف، فرمول اتحاد مزدوج به فارسی بهشکل زیر خواهد بود:
پیشنهاد مطالعه: اتحاد چاق و لاغر چیست؟
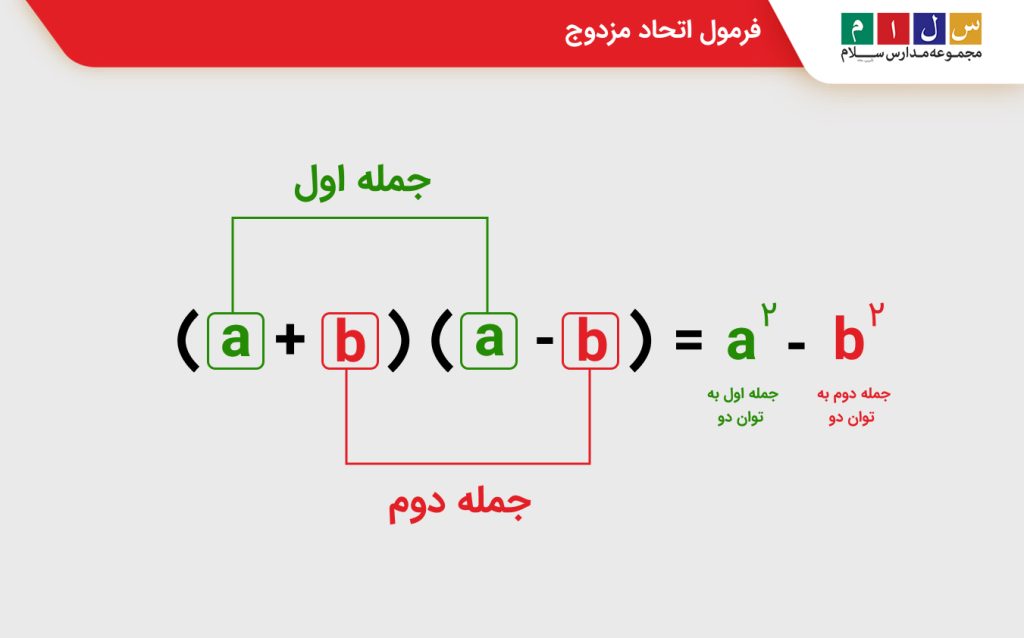
فرمول اتحاد مزدوج
براساس فرمول بالا اگر جمله اول را a و جمله دوم را b در نظر بگیریم، میتوانیم شکل جبری فرمول اتحاد مزدوج را بهصورت زیر نیز بنویسیم:
a۲– b۲ = ( a + b ) ( a – b)
اولین نفری باشید که از اخبار و اطلاعیههای مرتبط با پایه تحصیلیتان باخبر میشود!
اثبات اتحاد مزدوج
اثبات اتحاد مزدوج بسیار ساده است. کافیست از یک طرف تساوی شروع کنیم و به طرف دیگر تساوی برسیم. ابتدا اتحاد مزدوج را مینویسیم:
a + b) (a – b)=a۲– b۲)
از سمت چپ شروع کرده و جملههای a و b را بهصورت جداگانه در( a – b ) ضرب میکنیم:
a + b) ( a – b) =a (a – b) +b (a – b ))
=a۲– ab + ba – b۲
= a۲– b۲
همانطور که انتظار داشتیم سمت چپ تساوی بالا با سمت راست آن برابر شد و توانستیم فرمول اتحاد مزدوج را بهراحتی اثبات کنیم.
پیشنهاد مطالعه: اتحاد جمله مشترک چیست؟
تعبیر هندسی اتحاد مزدوج | اثبات اتحاد مزدوج هندسی
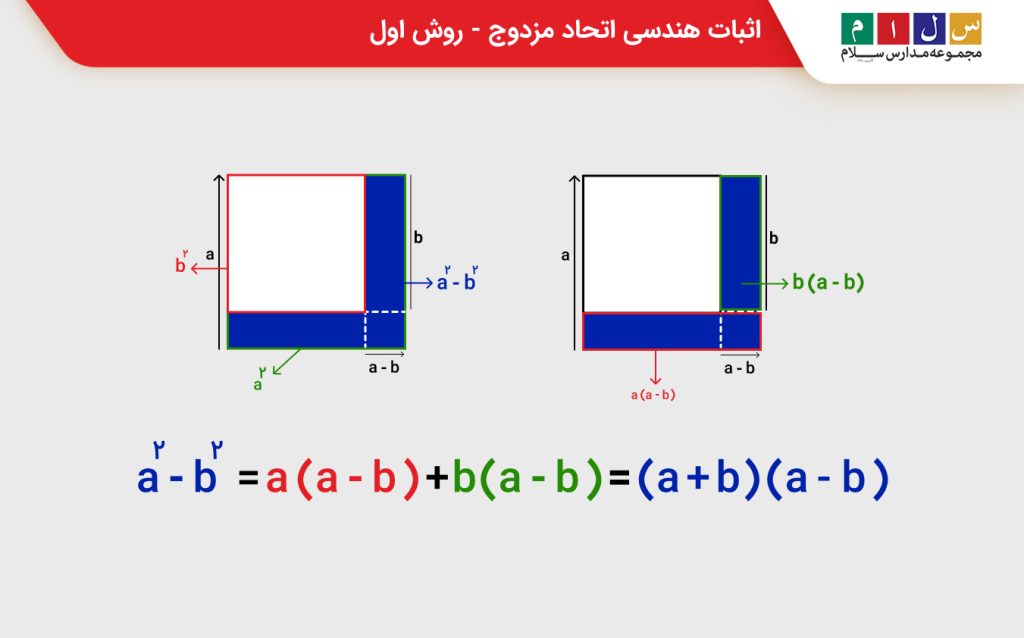
اتحاد مزدوج را میتوان بهصورت هندسی هم اثبات کرد و بهصورت تفاضل مساحت دو مربع نشان داد. به شکل زیر نگاه کنید. در این شکل، قسمتهای رنگشده، تفاضل مساحت دو مربع یعنی a۲-b۲ را نشان میدهند. مساحت این قسمتها را میتوان با جمع مساحت دو مستطیل نیز تعیین کرد که در این حالت به عبارت زیر خواهیم رسید:
( a (a – b) + b ( a – b
اگر از عبارت بهدستآمده فاکتور بگیریم، خواهیم داشت:
( a + b) ( a – b )
درنتیجه داریم:
a۲ – b۲ = ( a + b) ( a – b )
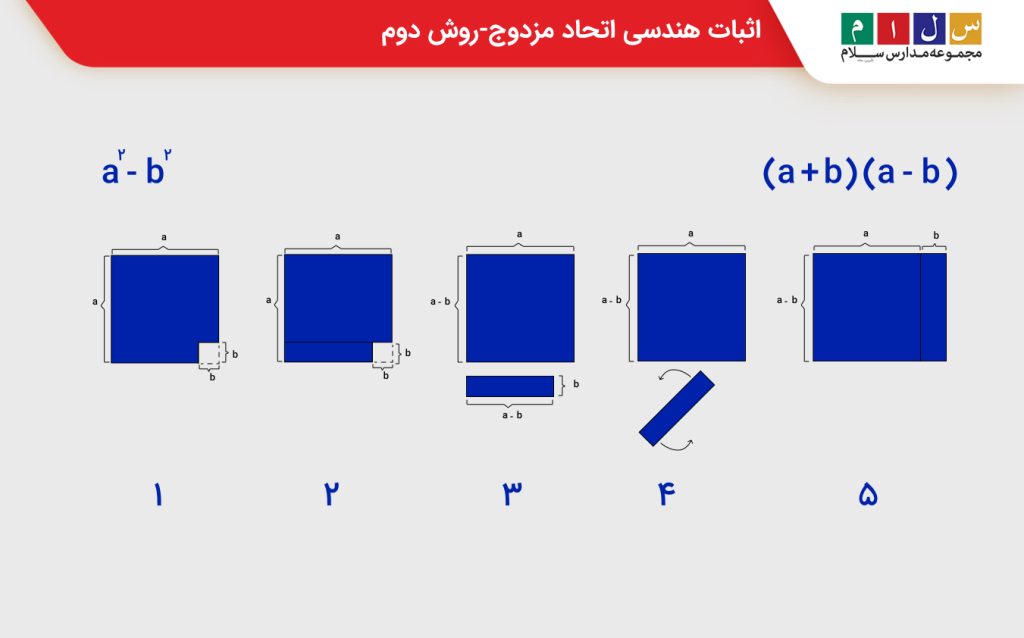
علاوهبر روش فوق، از روش هندسی دیگری نیز برای اثبات اتحاد مزدوج میتوان استفاده کرد.
فرض کنید یک مربع بزرگ به ضلع a داریم که یک مربع کوچک به ضلع b از آن جدا شده است. در این صورت، مساحت بخش رنگشده برابر با a۲-b۲ خواهد بود.
اکنون مطابق شکل شماره (۲) یک قطعه مستطیل را از قسمت پایین قطعه بزرگ جدا میکنیم. طول این مستطیل a-b و عرض آن b است. اگر این مستطیل را بچرخانیم و در سمت راست قطعه بزرگتر قرار دهیم، مستطیلی بزرگتر به طول a +b و عرض a-b خواهیم داشت که مساحت آن برابر است با
a + b) (a – b)) .
با توجه به اینکه تنها چیدمان شکل تغییر یافته است، میتوان نتیجه گرفت که مساحت شکل جدید برابر با مساحت شکل اولیه است. بنابراین، خواهیم داشت:
a۲ – b۲ = ( a + b) ( a – b )
نمونه سوال اتحاد مزدوج
سوال: حاصل عبارت ۵۲ -۸۲ را به کمک اتحاد مزدوج بهدست آورید.
جواب: این مسئله با استفاده از فرمول اتحاد مزدوج ریاضی نهم بهراحتی قابلحل است. کافیست عبارت دادهشده را بهصورت زیر تجزیه کنیم:
۸۲ – ۵۲ = (۸ – ۵) (۸ + ۵) =۳ × ۱۳ =۳۹
مثال تجزیه اتحاد مزدوج
تجزیه اتحادها یکی از پرکاربردترین روشها برای حل مسائل جبری است. در این بخش، برای آشنایی با شیوه تجزیه اتحاد مزدوج مثال ساده زیر را حل میکنیم.
۱۶ – x۲
برای تجزیه این عبارت، ابتدا باید به هر دو جمله دقت کنیم که آیا میتوان آنها را بهصورت مربع یک عدد (یا متغیر) نوشت یا نه. میدانیم که ۱۶ مجذور عدد ۴ است پس عبارت بالا را میتوان بهصورت زیر بازنویسی و تجزیه کرد:
۱۶ – x ۲= ۴۲– x۲= ( ۴ – x ) ( ۴ + x )
پیشنهاد مطالعه: اتحاد مکعب چیست؟
نمونه سوال تجزیه اتحاد مزدوج با جواب
با توجه به توضیح تجزیه اتحاد مزدوج ریاضی نهم ، درادامه این بخش چند مثال برای اتحاد مزدوج با جواب نهم متوسطه آورده شده است تا مطالب آموزشدادهشده برایتان بهتر جا بیفتد.
عبارتهای زیر را تجزیه کنید.
۱) y۲– ۵
۲) ۳۶a۲-c۲
۳) ۲x۲-۲۰۰
۴) ۸۱p۴-x۶
۵)
۶) ۲a۳b – ۸ab۳
تمام عبارتها را با استفاده از فرمول اتحاد مزدوج تجزیه میکنیم. نکتهای که هنگام تجزیه اتحاد مزدوج باید در نظر داشته باشید این است که اگر دو جمله عامل مشترک داشتند ابتدا از آن فاکتور بگیرید و سپس عبارت را تجزیه کنید. برای تجزیه اتحاد باید از جملهها جداگانه جذر بگیرید تا جملههای اول و دوم بهدست آیند.
۳) در این مثال، ابتدا از عامل مشترک دو جمله یعنی ۲ فاکتور میگیریم و سپس عبارت حاصل را تجزیه میکنیم:
( ۲x۲– ۲۰۰= ۲ (x۲-۱۰۰ ) = ۲ ( x + ۱۰ ) ( x – ۱۰
۴) ابتدا از هر دو جمله عبارت دادهشده جذر میگیریم تا جمله اول و دوم تعیین شود. داریم:
۵) در این مثال، عامل مشترک عدد ۳ است که با فاکتورگیری میتوان اتحاد را بهصورت زیر نوشت:
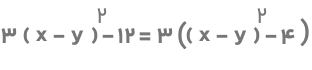
اکنون میتوانیم عبارت بالا را تجزیه کنیم:
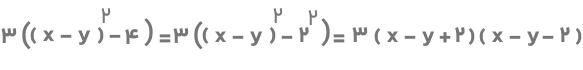
۶) از عامل مشترک ۲ab فاکتور میگیریم. خواهیم داشت:
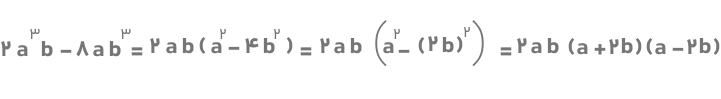
کاربرد اتحاد مزدوج در گویا کردن مخرج کسرها
زمانی که مخرج یک کسر دارای رادیکال است، میتوانیم با کمک اتحاد مزدوج رادیکال را حذف کنیم و آن را بهصورت گویا بنویسیم. به مثال زیر توجه کنید:
مخرج این کسر دارای رادیکال است و برای نوشتن آن بهصورت گویا کافیست صورت و مخرج کسر را در مزدوج عبارت مخرج ضرب کنیم:
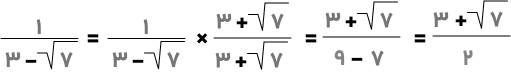
به این صورت میتوان رادیکال را از مخرج حذف کرد.
پیشنهاد مطالعه :اتحاد مربع
سخن پایانی
در این مطلب شما را با اتحاد مزدوج آشنا کردیم و کاربرد و نحوه اثبات آن را آموزش دادیم. با توجه به توضیح اتحاد مزدوج ریاضی نهم این اتحاد بیانگر یک تساوی است که نشان میدهد تفاضل مربع دو عدد (یا جمله) برابر با حاصلضرب مجموع دو عدد (یا جمله) در تفاضل آنهاست.
یادگیری اتحاد مزدوج و نحوه تجزیه آن در عبارتهای جبری، با حل تمرینهای گوناگون و متعدد امکانپذیر است. به همین خاطر توصیه میکنیم مسئلههای متفاوتی در این زمینه حل کنید تا بتوانید با شیوه استفاده از این اتحاد در مسائل بیشتر آشنا شوید.
سؤالات متداول
- اتحاد مزدوج چیست؟
اتحاد مزدوج یک تساوی است که در یک سمت آن تفاضل مربع دو جمله و در سمت دیگر آن حاصلضرب مجموع آن دو جمله در اختلاف آنها قرار میگیرد. - فرمول اتحاد مزدوج چیست؟
فرمول اتحاد مزدوج بهصورتاست.
- منظور از تجزیه اتحاد مزدوج چیست؟
منظور از تجزیه اتحاد مزدوج، نوشتن تفاضل مربع دو جمله بهصورت حاصلضرب مجموع دو جمله در تفاضل آن دو جمله است.