فهرست مطالب
Toggleانواع چهار ضلعی ها همهجا هستند و حتی همین حالا که این مطلب را میخوانید، یکی از آنها در قالب لپتاپ یا تلفن همراه مقابل دید شما قرار دارد! این اشکال هندسی از رایجترین اشکال به حساب میآیند و شما از لحظهای که به دنیا آمدهاید، هر روزه با آنها سروکار داشتهاید. حتی خواص چهار ضلعی ها را میشناسید؛ تنها به زبان ریاضی با آنها آشنایی ندارید! به همین دلیل ما این مطلب از مجموعه مدارس سلام، آشنایی و شناخت شما را با این خانواده از اشکال هندسی تکمیل می کند. در ادامه تعریف، خاصیت، اثبات، مثال و انواع چهار ضلعی ها را برای شما آوردهایم.
چهار ضلعی چیست؟
چهار ضلعی شکلی بسته در هندسه است که با اتصال چهار نقطه غیرهمخط به دست میآید. به زبان سادهتر، چهار ضلعی یک چندضلعی با چهار ضلع، چهار زاویه و چهار رأس است. به این ترتیب میتوان گفت هر روز اشیای زیادی میبینید که همین ساختار را دارند، مثل یک دفتر، یک تختهسیاه یا حتی یک قاب عکس روی دیوار.
نکته مهم در نامگذاری این اشکال، ترتیب رأسهاست. اگر شکلی را با چهار نقطه A,B,C,DA, B, C, DA,B,C,D بسازیم، باید آن را در یکی از حالتهای ABCD، BCDA، ADCB یا DCBA نامگذاری کنیم. نامهایی مانند ACBD یا DBAC اشتباه هستند، چون ترتیب اتصال رأسها را بر هم میزنند.

در این شکل چهار ضلع داریم:AB ، BC، CD و DA و همچنین دو قطر AC و BD که نقاط غیرمجاور را به هم وصل میکنند.
پیشنهاد مطالعه : ذوزنقه قائم الزاویه
قسمت های مختلف چهار ضلعی
برای اینکه محیط یا مساحت یک چهار ضلعی را محاسبه کنید یا بتوانید شکل آن را دقیقتر بشناسید، باید اجزای اصلی آن را بلد باشید. این اجزا همیشه در همه چهارضلعیها مشترک هستند:
- زاویهها: چهار زاویه که در رأسهای شکل قرار میگیرند: A، <B، <C ، <D >
- ضلعها: چهار پارهخط که شکل را میسازند: AB، BC، CD و DA.
- رأسها: چهار نقطهای که اضلاع به آنها ختم میشوند: A، B، C و D.
- قطرها: دو پارهخط که رأسهای غیرمجاور را به هم وصل میکنند: AC و BD.
این اجزا همان چیزهایی هستند که در همه مسائل مربوط به چهارضلعی ها با آنها سروکار داریم، چه بخواهیم محیط حساب کنیم و چه مساحت یا حتی زاویهها را بررسی کنیم.

خواص چهار ضلعی
ویژگی چهار ضلعی ها باید حتماً در یک شکل هندسی وجود داشته باشد تا بتوان آن شکل را در این خانواده قرار داد. حتی اگر یکی از این ویژگیها در شکل نباشد، نمیتوان آن را چهار ضلعی نامید. از این رو پیش از آنکه سراغ انواع مختلف چهار ضلعی برویم، بهتر است ویژگیهای اصلی این شکلها را مرور کنیم. این خواص تقریباً در همه چهار ضلعیها یکسان است و دانستن آنها برای حل تمرینها ضروری است:
- چهار ضلع، چهار زاویه و چهار رأس دارد.
- مجموع زاویههای داخلی همیشه برابر با ۳۶۰ درجه است.
- دو قطر دارد که رأسهای غیرمجاور را به هم وصل میکنند.
- منظم یا نامنظم است. در یک چهار ضلعی منظم، همه ضلعها برابرند، همه زاویهها ۹۰ درجه هستند و قطرها همدیگر را نصف میکنند.
سادهترین مثالی که میتوانیم برای تمامی این ویژگیها در نظر بگیریم، شکل مربع است که یک چهار ضلعی منظم به آن میگویند چراکه تمامی اضلاع، زوایا و قطرها یک اندازه هستند.
اولین نفری باشید که از اخبار و اطلاعیههای مرتبط با پایه تحصیلیتان باخبر میشود!
انواع چهار ضلعی ها
همانطور که اشاره کردیم، انواع چهار ضلعی ها فقط یک شکل ثابت نیستند و خانواده بزرگی از شکلهای مختلف را شامل میشوند که هر کدام ویژگیهایی دارند. بعضی از آنها زاویههای قائمه دارند، بعضی همه ضلعهایشان برابر است و بعضی تنها یک جفت ضلع موازی دارند. شناخت این دستهها کمک میکند تا راحتتر شکلها را تشخیص بدهید و مسائل مربوط به آنها را حل کنید.
مستطیل
مستطیل یکی از آشناترین انواع چهار ضلعی محسوب میشود چراکه کتابها، صفحه گوشی و حتی تختهسیاه کلاس همه شکل مستطیل دارند. در مستطیل، ضلعهای روبهرو موازی و مساوی بوده و همه زاویهها دقیقاً ۹۰ درجه هستند. به همین دلیل مستطیل همیشه چهار زاویه قائمه دارد. همچنین قطرهای مستطیل هم برابر هستند. به طور کلی این چهار ضلعی را میتوانیم دوقلوی ناهمسان متوازی الاضلاع بدانیم!

بر اساس این تصویر، اثبات و روابط موجود مستطیل را میتوانیم به این شکل بنویسیم:
پیشنهاد مطالعه: نحوه محاسبه محیط مستطیل و محاسبه مساحت مستطیل
متوازیالاضلاع
متوازیالاضلاع شکلی است که ضلعهای روبهرو در آن موازی و مساوی هستند. به این معنا که اگر دو ضلع روبهروی هم را امتداد بدهید، هیچ وقت به هم نمیرسند و فاصلهشان یکسان است. علاوه بر این، زاویههای مخالف در متوازیالاضلاع هم برابر هستند. مربع، مستطیل و لوزی نمونههایی از متوازیالاضلاع به حساب میآیند چراکه همه آنها این ویژگی اصلی را دارند.

بر اساس این تصویر میتوانیم بگوییم که در چهار ضلعی متوازیالاضلاع رابطه زیر برقرار است:
مربع
مربع در واقع ترکیبی از ویژگیهای مستطیل و لوزی است. هر چهار ضلعش برابر و هر چهار زاویهاش هم ۹۰ درجه هستند. به همین خاطر هم منظمترین نوع چهار ضلعی شناخته میشود. وقتی روی کاشیهای کف اتاق یا صفحه شطرنج نگاه میکنید، دهها مربع مقابلتان قرار دارد.

بر اساس این تصویر، یک چهار ضلعی مربع با رابطه زیر مربع است:
ذوزنقه
ذوزنقه شکلی است که تنها یک جفت ضلع موازی دارد و البته به طور معمول این جفت ضلع موازی، هم اندازه نیستند. همین ویژگی باعث میشود ظاهرش با بقیه چهارضلعیها متفاوت باشد. در ذوزنقه، مجموع زاویههای مجاور بین دو ضلع غیرموازی برابر با ۱۸۰ درجه است.

بر اساس این تصویر، رابطه زیر در ذوزنقه برقرار است:
پیشنهاد مطالعه: مساحت ذوزنقه چیست؟
لوزی
لوزی هم مثل مربع چهار ضلع مساوی دارد، اما زاویههایش قائمه نیستند. در لوزی هم با اندازهها و ضلعهای یکسان مثل مربع مواجه هستیم. در واقع زاویههای روبهرو در لوزی برابر هستند، ولی یکی از زاویهها تندتر و دیگری بازتر از ۹۰ درجه است. به همین دلیل میتوان گفت هر مربع یک لوزی است، اما هر لوزی الزاماً مربع نیست.

در این تصویر از لوزی به عنوان یک چهار ضلعی، این موارد با برابری موجب ایجاد یک چهار ضلعی شدهاند:
کایت
کایت یا بادبادک هم با شکل و ظاهر خاص خود یکی از انواع چهارضلعی است که گاهی در برخی منابع و کتابها از قلم میافتد! در این شکل، دو ضلع مجاور آن برابر و یک جفت زاویه روبهرو هم با هم مساوی هستند.

در این تصویر هم که کایت یا بادبادک وجود دارد، رابطه زیر باعث شده تا از خاصیت چهار ضلعی برخوردار باشد:
چهار ضلعی محدب و مقعر
علاوه بر انواع چهار ضلعی مذکور، چهارضلعیها را میتوان بر اساس زاویههای داخلی هم دستهبندی کرد.
- چهار ضلعی محدب: همه زاویههای داخلی کوچکتر از ۱۸۰ درجه هستند و هر دو قطر داخل شکل قرار میگیرند. بیشتر شکلهایی که در زندگی روزمره میبینید، از همین نوع هستند.
- چهار ضلعی مقعر: یکی از زاویهها بزرگتر از ۱۸۰ درجه است و دستکم یکی از قطرها از شکل بیرون میافتد. این نوع کمتر رایج است و بیشتر در ترسیمات خاص هندسی دیده میشود.

جدول ویژگی های چهار ضلعی ها
| متوازیالاضلاع | مستطیل | مربع | لوزی | ذوزنقه | کایت | |
| همه زوایا برابر | ✓ | ✓ | ✓ | |||
| زوایای مخالف برابر | ✓ | ✓ | ✓ | ✓ | ||
| همه زوایا ۹۰ درجه | ✓ | ✓ | ✓ | |||
| اضلاع مخالف برابر | ✓ | ✓ | ✓ | ✓ | ||
| قطرها منصف | ✓ | ✓ | ✓ | ✓ | ✓ | |
| قطرها برابر | ✓ | ✓ | ✓ |
اثبات چهار ضلعی
به طور کلی شما میتوانید بر اساس روابط و خاصیت چهار ضلعی که بیان کردیم، چهار ضلعی بودن اشکال مختلف از مربع و مستطیل تا ذوزنقه و لوزی را اثبات کنید. به عنوان نمونه، در این قسمت نحوه اثبات برابری زوایا، قطرها و اضلاع را در متوازیالاضلاع آوردهایم.
مرحله اول: اثبات موازی و برابر بودن دو ضلع مقابل
- همانطور که گفتیم، در یک متوازیالاضلاع دو ضلع مقابل باید موازی باشند.
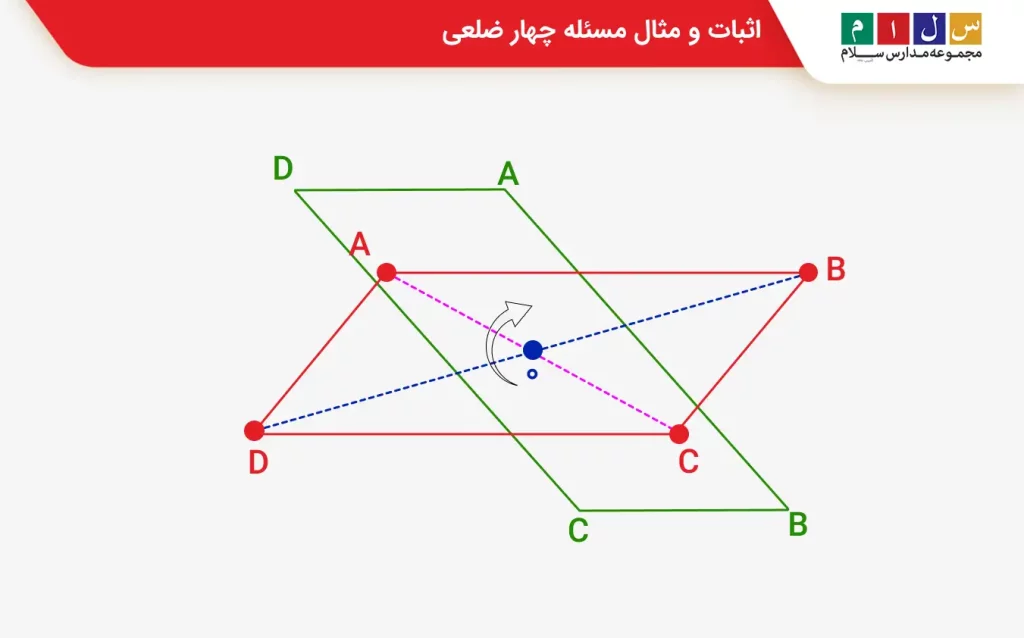
2.از آنجا که این رابطه در شکل وجود دارد:
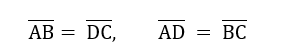
- میتوانیم بگوییم دو ضلع موازی هستند و این قانون چهار ضلعی متوازیالاضلاع برقرار است. برای راحتتر شدن این مسئله، میتوانید شکل را ۱۸۰ درجه بچرخانید و سپس بررسی کنید.
مرحله دوم: اثبات نصف شدن قطرها
۱. در این قسمت باید نشان دهیم که قطرها یکدیگر را نصف میکنند.
۲. پس از آنکه شکل را ۱۸۰ درجه میچرخانیم مشخص میشود که:
۳. در نتیجه همانطور که باید، قطرها هم یکدیگر را نصف کرده و دوبهدو برابر هستند.
مرحله سوم: جمع زوایا
- جمع زوایای متوازیالاضلاع به عنوان یک چهارضلعی باید ۳۶۰ درجه باشد.
- زوایای روبهرو در شکل دادهشده برابر هستند و اگر آنها را جمع کنیم، ۳۶۰ به دست میآید.
- سپس مکمل بودن زوایای متوازیالاضلاع را با این فرمول به دست میآوریم و اثبات انجام میشود:
دستهبندی چهار ضلعی ها
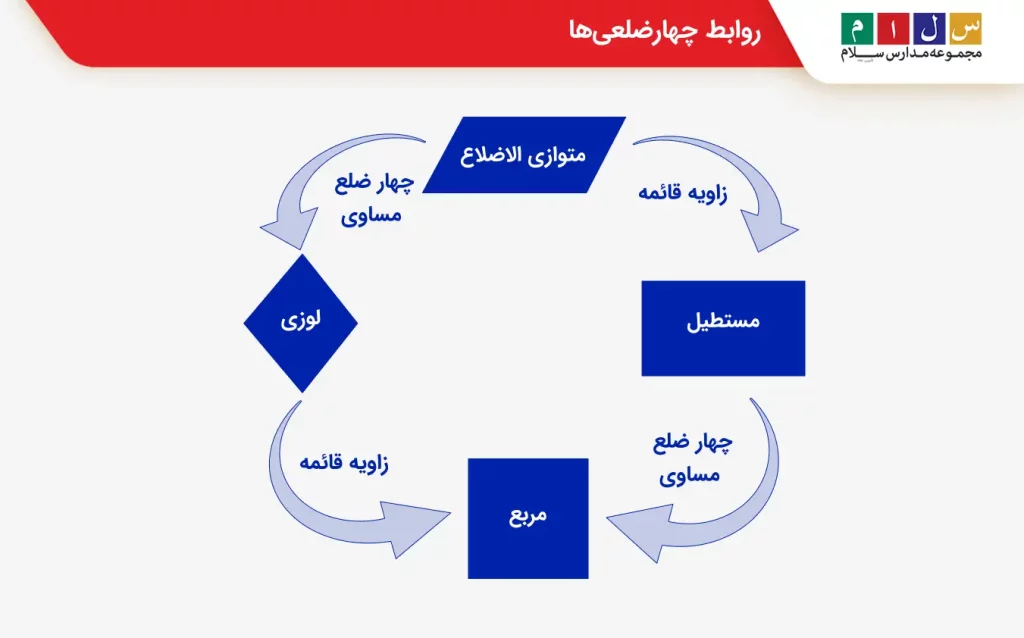
با کمک نمودار درختی چهار ضلعی میتوان روابط میان آنها را بهتر فهمید. برای نمونه، مربع نوعی مستطیل و در عین حال نوعی لوزی است، اما همه مستطیلها یا لوزیها مربع محسوب نمیشوند. همینطور مشخص میشود که مستطیلها کایت نیستند. در واقع این نمودار نشان میدهد چگونه تعریف هر شکل به شکل دیگر مرتبط میشود و با دقت به فلشها میتوان به بسیاری از پرسشهای مربوط به چهارضلعیها پاسخ داد.

در کنار این، رابطه خاصی هم بین چهار ضلعی مربع، مستطیل، متوازیالاضلاع و لوزی هم برقرار است که در تصویر زیر نشان دادهایم.
تمرین از چهار ضلعی
در این بخش هم مثالهایی از چهار ضلعی در امتحانات و کتابهای ریاضی مدارس را بررسی میکنیم تا بتوانید با مطالعه آنها به عنوان نمونه سؤال، درک بهتری از آنها پیدا کنید.
- مثال اول
از وصل کردن وسط اضلاع مربع ABCD چهار ضلعی PQRS به دست آمده است. مشخص کنید PQRS چه نوع چهارضلعیای است.
- در ابتدا روی هر ضلع مربع نقطه وسط را مشخص کنید:
P وسط AB، Q وسط BC، R وسط CD و S وسط DA.

- اگر پس از تا زدن، همه ضلعها برابر باشند، شکل به دست آمده لوزی است.
- اگر زاویهها روی هم بیفتند، شکل به دست آمده مستطیل است.
- اگر هم ضلعها برابر باشند و هم زاویهها ۹۰ درجه شوند، در این صورت شکل مربع خواهد بود.
- حالا مربع ABCD را در نظر بگیرید و آن را روی خطوط تقارنش تا بزنید:

۶.وقتی مربع را روی خطوط تقارن وسط اضلاع تا میزنیم، میبینیم که همه ضلعهای PQRS روی هم قرار میگیرند. این نشان میدهد که تمام ضلعهای PQRS با هم برابر هستند. در نتیجه PQRS یک لوزی است.
- مثال دوم
در کتاب ریاضی پنجم یک شکل متوازیالاضلاع آمده و با یک زاویه 110 درجه، خواسته شده که باقی زوایا به دست آیند.

برای اثبات چهار ضلعی از این طریق، مراحل زیر را طی میکنیم:
- در ابتدا باید بدانیم که در متوازیالاضلاع، ضلعهای روبهرو موازی هستند و زاویههای روبهرو برابر هستند. همچنین دو زاویه کنار هم یا مجاور، مکمل هستند، یعنی مجموعشان 180 درجه است.
- یک زاویه متوازیالاضلاع برابر 110 درجه داده شده است.
- بر این اساس، زاویه کنار آن برابر است با:
180 – 110 = 70
- زاویههای روبهروی هر زاویه با خودش برابر است که در نتیجه:
زاویه روبهروی 110 درجه → دوباره 110 درجه
زاویه روبهروی 70 درجه → دوباره 70 درجه
- بر اساس همین مراحل ساده، زاویههای متوازیالاضلاع به ترتیب به این شرح هستند:
110,70,110,70
| یادآوری: اگر دقت کنید، جمع کلیه زوایا هم 360 است که از خواص چهار ضلعی ها محسوب میشود. |
جمعبندی
چهار ضلعی ها در واقع خانوادهای بزرگ از شکلهای هندسی هستند که ویژگیهای مشابه و متفاوتی دارند. برای مثال مربع هم لوزی است و هم مستطیل اما برعکسش درست نیست چون هر لوزی یا مستطیل لزوما مربع نمیشود. در متوازیالاضلاع زاویههای روبهرو برابر و زاویههای کنار هم مکمل هستند، در ذوزنقه تنها یک جفت ضلع موازی داریم و در کایت دو ضلع مجاور مساوی هستند. اگر به نمودار درختی نگاه کنیم، میبینیم که همه این شکلها به هم مربوط هستند. تنها باید تعریف هر کدام را به یاد داشته باشیم تا بتوانیم به راحتی به پرسشهای مربوط به ویژگی های چهار ضلعی و اثبات آنها پاسخ بدهیم.
سؤالات متداول
- کامل ترین شکل از لحاظ هندسی کدام چهار ضلعی است؟
مربع است چون 4 ضلع و 4 زاویه برابر دارد. - چهار ضلعی که چهار زاویه برابر و چهار ضلع مساوی دارد چه نام دارد؟
چهارضلعی که چهار زاویه برابر و چهار ضلع مساوی دارد مربع است. - چهار ضلعی که فقط یک زاویه باز دارد؟
ذوزنقه از نوع قائمالزاویه چهار ضلعی که فقط یک زاویه باز دارد، محسوب میشود. - چهار ضلعی که مرکز تقارن ندارد؟
تنها ذوزنقه این ویژگی را دارد.

















