فهرست مطالب
Toggleاهرام ثلاثه مصر نمونههای آشنایی از شکل هرم هستند. اگر تصویر این اهرام باستانی را دیده باشید، متوجه میشوید که همه آنها از وجههای مثلثیشکل ساخته شدهاند. در ریاضی هرم به اشکالی سهبعدی گفته میشود که از وجههایی بهشکل مثلث تشکیل شده باشند. برای اینکه با این شکل هندسی بیشتر آشنا شوید، در ادامه این مطلب ابتدا شما را با معنی هرم در ریاضی آشنا میکنیم و سپس، به معرفی اجزا و سایر ویژگیهای این حجم هندسی میپردازیم.
هرم چیست؟
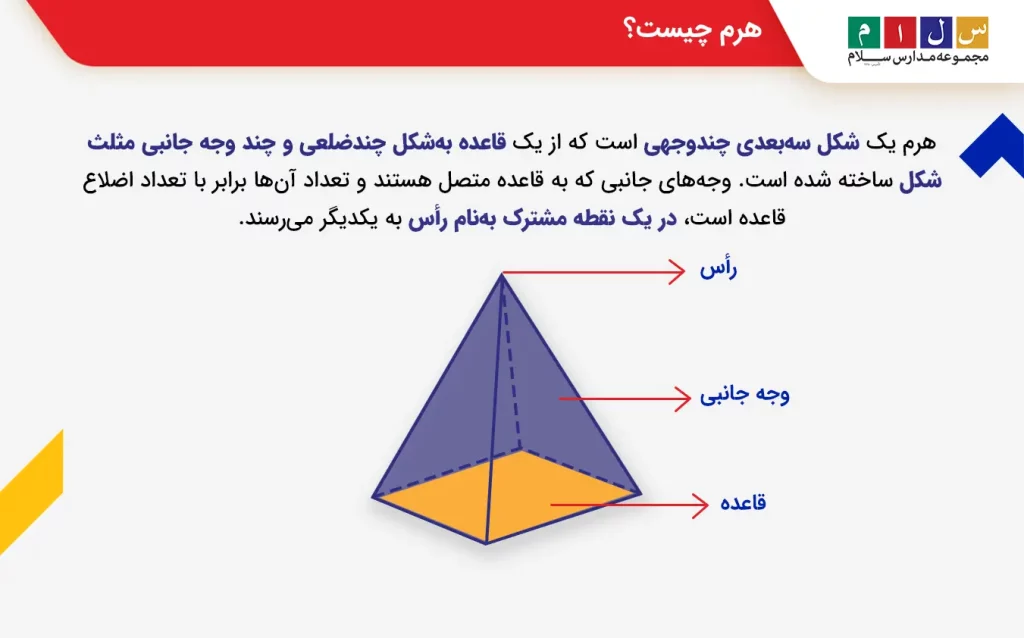
هرم یک شکل سهبعدی چندوجهی است که از یک قاعده بهشکل چندضلعی و چند وجه جانبی مثلثشکل ساخته شده است. وجههای جانبی که به قاعده متصل هستند و تعداد آنها برابر با تعداد اضلاع قاعده است، در یک نقطه مشترک بهنام رأس به یکدیگر میرسند. رأس در بالای قاعده قرار دارد.
اجزای هرم
تا اینجا یک تعریف کلی از شکل هرم ارائه کردیم. اکنون میخواهیم اجزای مختلف یک هرم را معرفی کنیم. اجزای هرم عبارتاند از:
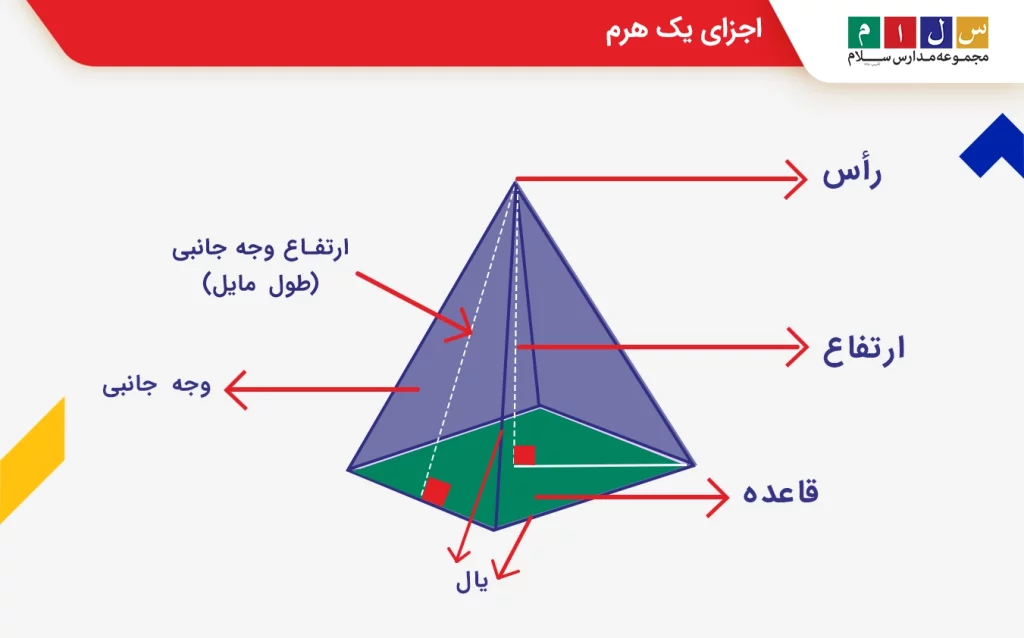
- رأس: نقطه مشترکی که وجههای مثلثی به آن منتهی میشوند و در بالای قاعده قرار دارد. البته هرم رأسهای دیگری نیز دارد که از برخورد قاعده با دو وجه جانبی ایجاد میشوند و در پایین هرم قرار دارند.
- قاعده: وجه مسطحی که رأس در بالای آن قرار میگیرد و میتواند بهشکل یک سهضلعی، چهارضلعی، پنجضلعی و غیره باشد.
- وجههای جانبی: سطوح صاف مثلثشکلی که به قاعده متصل هستند و در رأس به هم میرسند.
- یال: محل اتصال دو وجه را یال یا لبه میگویند.
- ارتفاع: پارهخطی که از رأس آغاز میشود و انتهای دیگر آن بر قاعده عمود است. بهعبارت دیگر، ارتفاع هرم برابر است با فاصله عمودی رأس و قاعده آن.
- طول مایل: منظور از طول مایل، ارتفاع وجه جانبی است.
اولین نفری باشید که از اخبار و اطلاعیههای مرتبط با پایه تحصیلیتان باخبر میشود!
انواع هرم
هرمها براساس موقعیت رأس نسبت به مرکز قاعده و اندازه اضلاع قاعده به انواع گوناگونی دستهبندی میشوند.
انواع هرم ازنظر موقعیت رأس نسبت به مرکز قاعده:
- هرم قائم
- هرم مایل
انواع هرم ازنظر اندازه اضلاع قاعده:
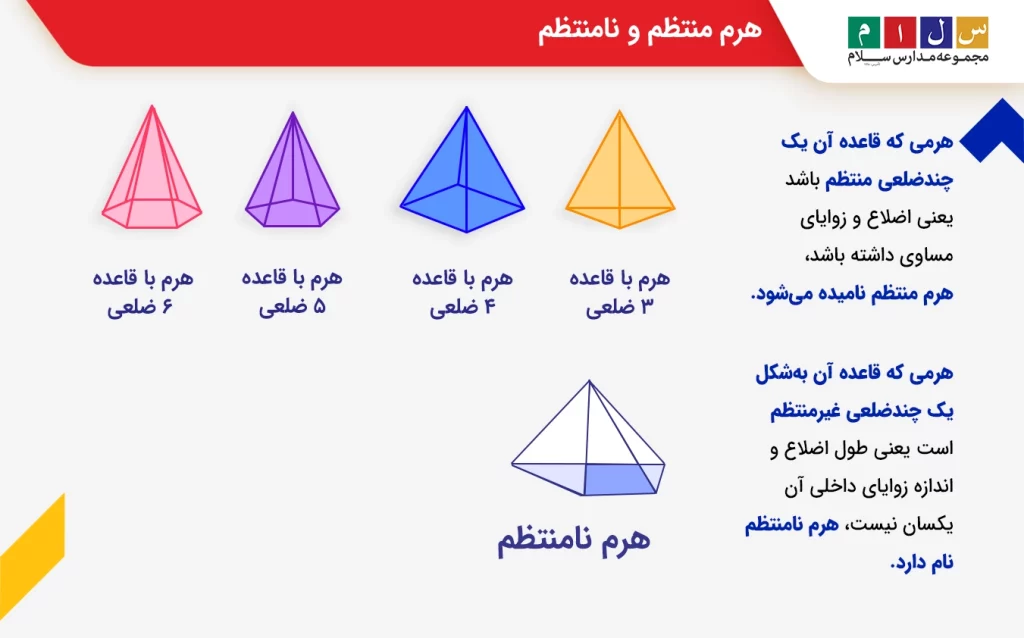
- هرم منتظم
- هرم نامنتظم
هرم منتظم و نامنتظم
هرمی که قاعده آن یک چندضلعی منتظم باشد یعنی اضلاع و زوایای مساوی داشته باشد، هرم منتظم نامیده میشود. اما هرمی که قاعده آن بهشکل یک چندضلعی غیرمنتظم است یعنی طول اضلاع و اندازه زوایای داخلی آن یکسان نیست، هرم نامنتظم نام دارد.
نکته: در هرم منتظم تمام وجههای جانبی هماندازه هستند.
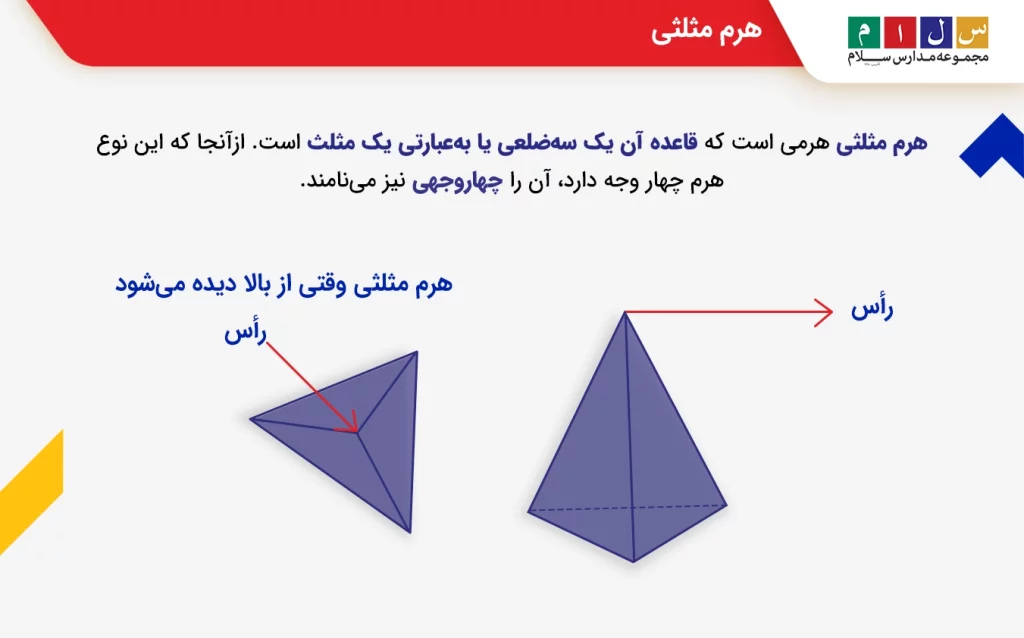
هرم مثلثی
هرم مثلثی هرمی است که قاعده آن یک سهضلعی یا بهعبارتی یک مثلث است. ازآنجا که این نوع هرم چهار وجه دارد، آن را چهاروجهی نیز مینامند.
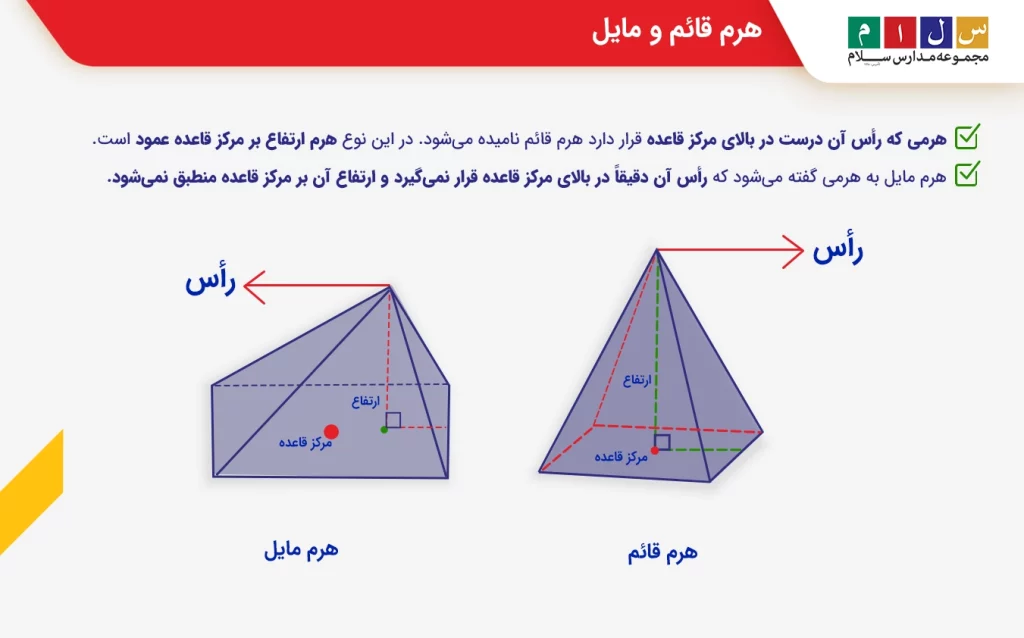
هرم قائم و مایل
هرمی که رأس آن درست در بالای مرکز قاعده قرار دارد هرم قائم نامیده میشود. در این نوع هرم ارتفاع بر مرکز قاعده عمود است.
هرم مایل به هرمی گفته میشود که رأس آن دقیقاً در بالای مرکز قاعده قرار نمیگیرد و ارتفاع آن بر مرکز قاعده منطبق نمیشود.
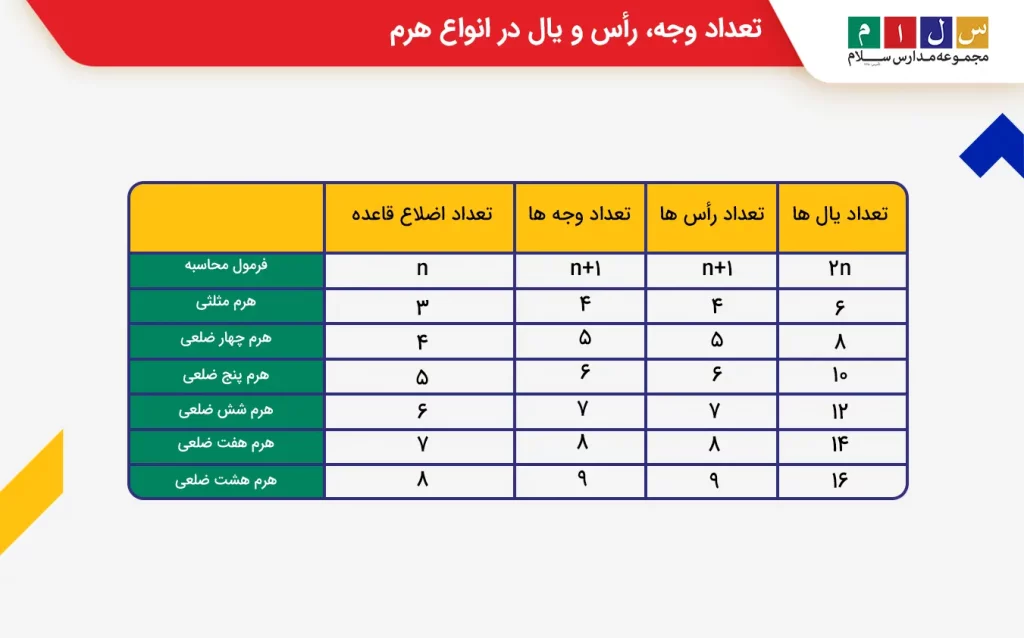
تعداد وجه ها، رأس ها و یال ها در انواع هرم
هرمی با قاعده nضلعی، n+1 وجه، n+1 رأس و 2n یال دارد. بهعنوان مثال، در هرمی با قاعده مربعی (n=4)، ۵ وجه (۱+۴)، ۵ رأس (۱+۴) و ۸ یال (۴×۲) وجود دارد. در جدول زیر، تعداد وجه، رأس و یالهای هرمهای مختلف آورده شده است.
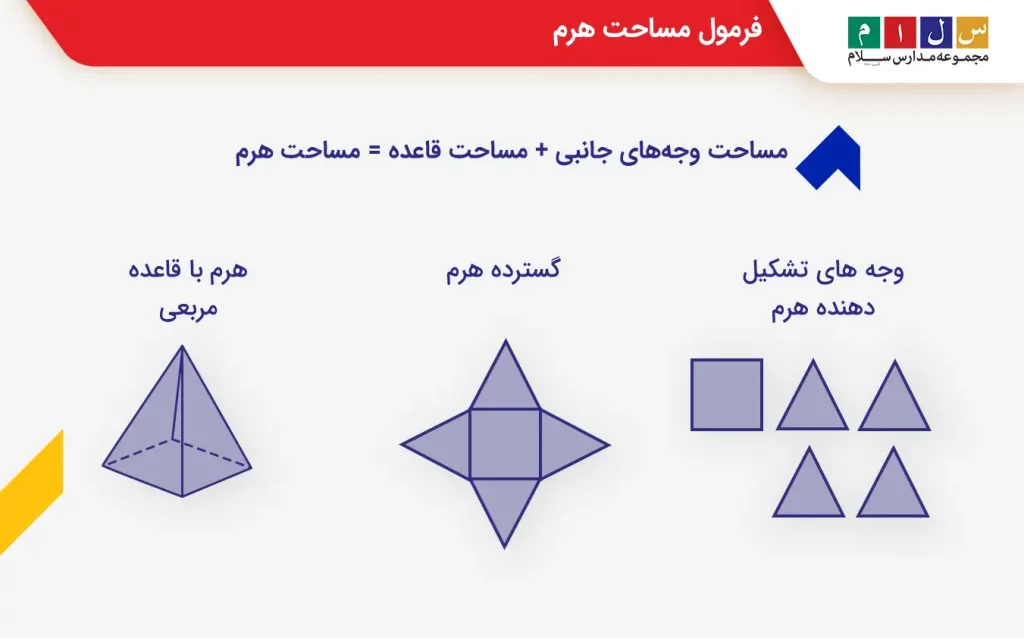
مساحت هرم
مساحت هرم از مجموع مساحت تمام وجههای آن بهدست میآید. با توجه به اینکه هرم از چند وجه ساخته شده است، بهتر است برای درک بهتر شکل و دوری از اشتباه در شمارش وجهها، آن را در یک صفحه گسترده کنیم. برای مثال، اگر یک هرم مربعی را بهصورت زیر گسترده کنیم، میتوانیم تعداد و شکل وجههای آن را بهخوبی ببینیم.
بهطور کلی، مساحت یک هرم را میتوان از فرمول زیر بهدست آورد:
مساحت وجههای جانبی + مساحت قاعده = مساحت هرم
مثال: مساحت هرم زیر را بهدست آورید.
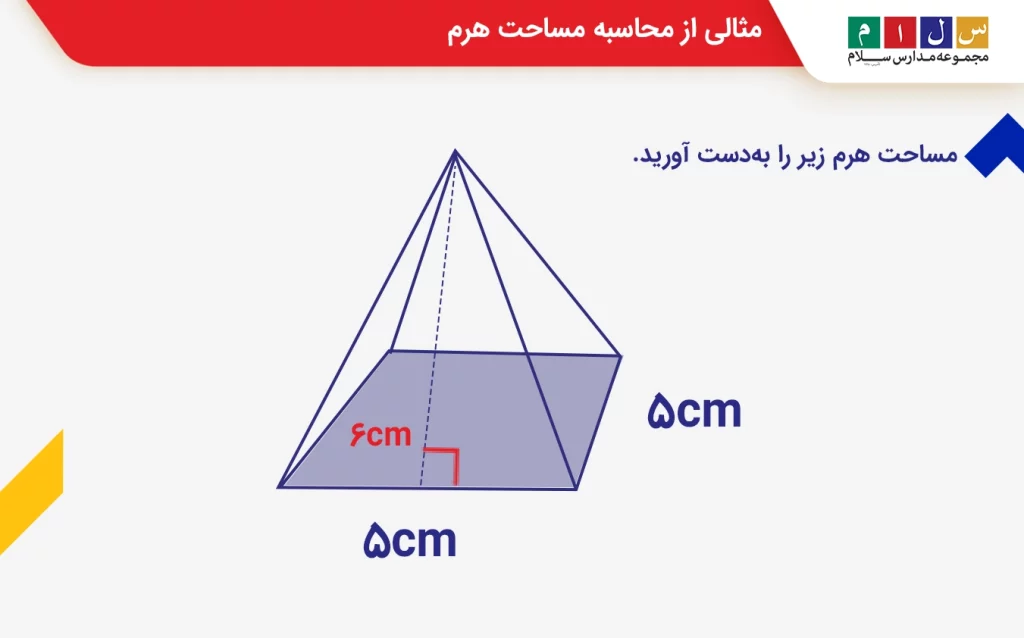
جواب: هرم دادهشده یک هرم با قاعده مربعی و وجههایی هماندازه بهشکل مثلث متساوی الساقین است. با توجه به فرمول مساحت هرم، ابتدا مساحت قاعده مربعی را محاسبه میکنیم. داریم:
خودش × یک ضلع = مساحت قاعده مربعی
۲۵ سانتیمتر مربع = ۵ × ۵ = مساحت قاعده مربعی
ازآنجا که قاعده این هرم قائم بهشکل مربع است، چهار وجه جانبی آن یکسان خواهد بود. بنابراین، برای محاسبه مساحت جانبی هرم ابتدا مساحت یکی از وجههای مثلثی را بهدست میآوریم و سپس حاصل آن را در ۴ ضرب میکنیم. خواهیم داشت:
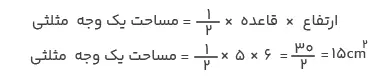
درنتیجه مساحت جانبی هرم برابر است با
مساحت یک وجه مثلثی × ۴ = مساحت جانبی هرم
۶۰ سانتیمتر مربع = ۱۵ × ۴ = مساحت جانبی هرم
بنابراین، مساحت کل هرم بهصورت زیر خواهد بود:
مساحت جانبی + مساحت قاعده = مساحت هرم
۸۵ سانتیمتر مربع = ۶۰ + ۲۵ = مساحت هرم
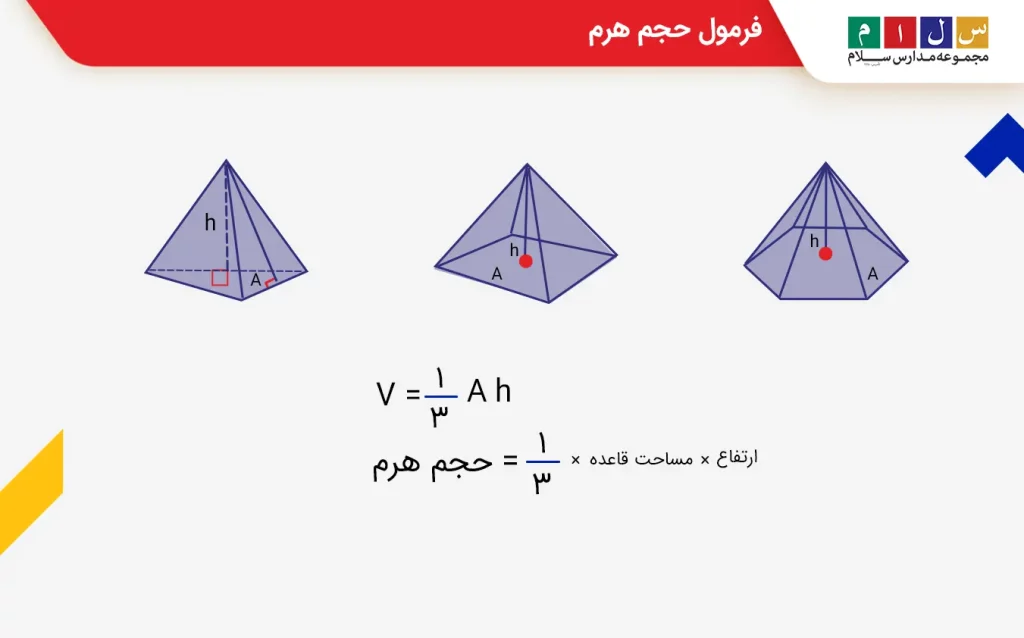
حجم هرم
به فضای اشغالشده بین وجههای هرم حجم هرم میگویند. حجم هرم برابر است با «یکسوم حاصلضرب مساحت قاعده در ارتفاع».
مثال: حجم هرم زیر را محاسبه کنید.
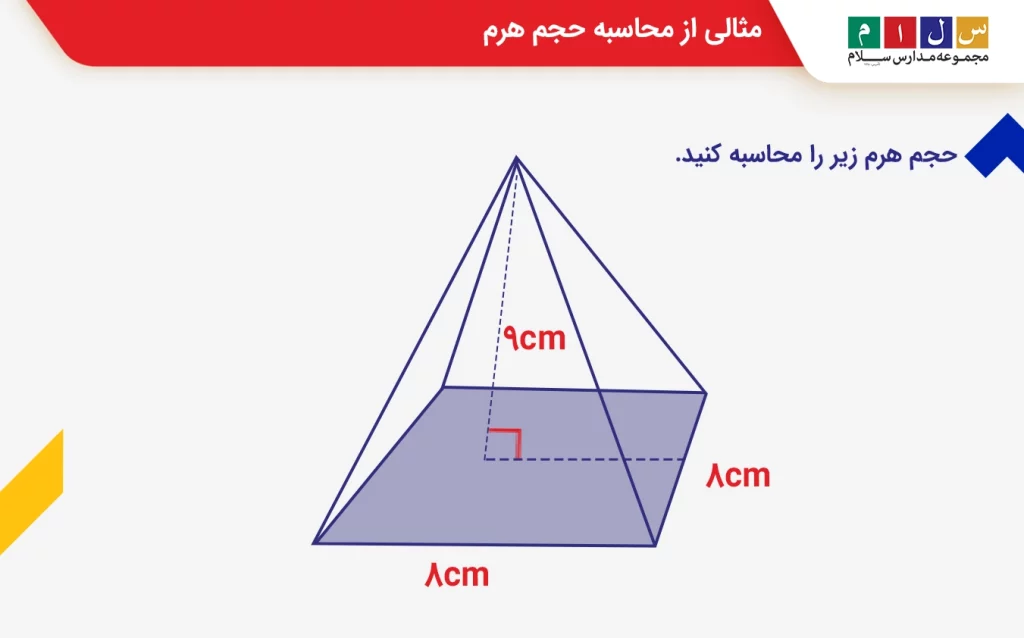
جواب: با توجه به فرمول حجم هرم، رای محاسبه حجم این شکل هندسی باید مقدار مساحت قاعده را تعیین کنیم. قاعده بهشکل مربع است و مساحت آن برابر است با
خودش × یک ضلع = مساحت قاعده
۶۴ سانتیمتر مربع = ۸ × ۸ = مساحت قاعده
اکنون با جایگذاری مقدار مساحت قاعده و ارتفاع در فرمول بالا، حجم هرم را بهدست میآوریم:

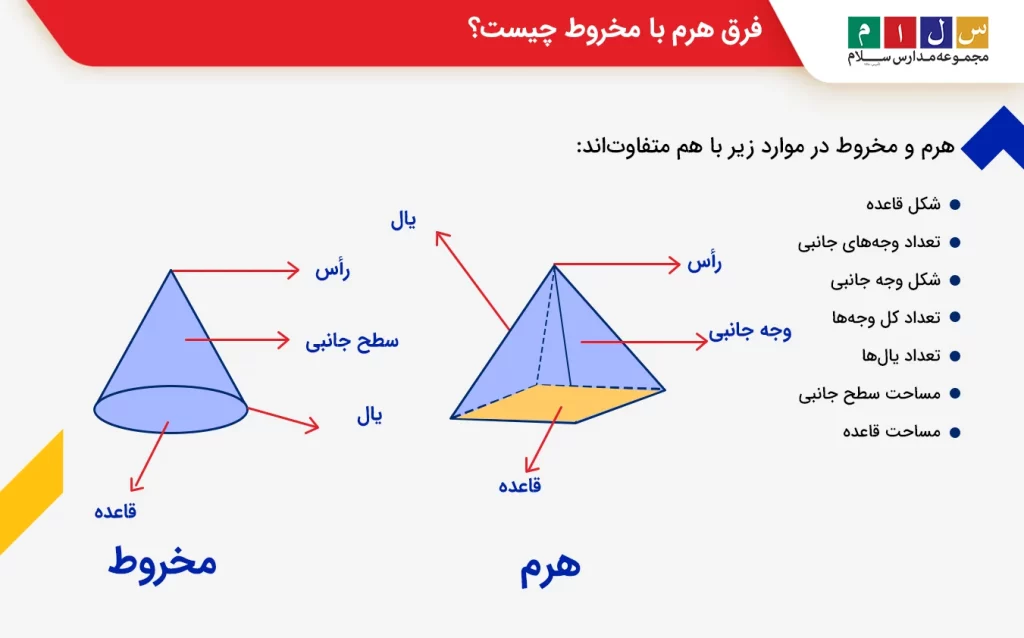
فرق هرم با مخروط
هرم و مخروط دو شکل هندسی شبیه به هماند؛ هر دوی آنها دارای یک قاعده و یک رأس در مقابل قاعده هستند. این دو حجم هندسی در موارد زیر با هم تفاوت دارند:
- تعداد یالها
- تعداد وجههای جانبی
- تعداد کل وجهها
- شکل وجه جانبی
- شکل قاعده
- مساحت قاعده
- مساحت سطح جانبی
اگر علاقهمند هستید راجعبه تفاوت و شباهت هرم و مخروط بیشتر بدانید، توصیه میکنیم مقاله فرق هرم با مخروط را مطالعه کنید. در آنجا موارد بالا را برای هر یک از این دو شکل هندسی توضیح دادهایم.
سخن پایانی
در این مطلب شکل هرم و اجزای آن را معرفی کردیم و گفتیم که هرم یک شکل سهبعدی چندوجهی شامل یک قاعده و چند وجه جانبی مثلثیشکل است. وجههای مثلثی در یک نقطه بهنام رأس که در بالای قاعده قرار دارد به هم میرسند و همگی به اضلاع قاعده متصل هستند. هرمها انواع مختلفی دارند که در این مقاله همراه با شکل درمورد ویژگیهای هر یک توضیح دادیم. همچنین درمورد روش محاسبه مساحت و حجم هرم صحبت کردیم. توصیه میکنیم برای تسلط بیشتر بر نحوه محاسبه مساحت و حجم هرم، هرمهایی با قاعدههای مختلف را انتخاب کنید و مساحت و حجم آنها را بهدست آورید. با این کار یادگیری شما عمیقتر خواهد شد.
سؤالات متداول
- هرم در ریاضی یعنی چه؟
هرم یک چندوجهی است که از یک قاعده چندضلعی و چند وجه جانبی مثلثی ایجاد شده است. - قاعده هرم چیست؟
قاعده هرم یک چندضلعی است که تمام وجههای جانبی به آن متصل هستند. - هرم چند قاعده دارد؟
هرم تنها یک قاعده دارد. - هرم چند وجه دارد؟
تعداد وجههای هرم بستگی به شکل قاعده آن دارد. - انواع هرم را نام ببرید.
هرمها براساس محل قرارگیری رأس نسبت به مرکز قاعده به دو دسته هرم قائم و مایل و براساس اندازه اضلاع قاعده به دو نوع منتظم و نامنتظم تقسیمبندی میشوند. - فرمول مساحت هرم چیست؟
مساحت هرم برابر است با حاصلجمع مساحت تمام وجههای آن. - فرمول حجم هرم چیست؟
حجم هرم از فرمول «یکسوم حاصلضرب مساحت قاعده در ارتفاع» تعیین میشود.









