فهرست مطالب
Toggleحتماً تابهحال در اخبار و رسانهها بسیار دیده و شنیدهاید که هواشناسی در برخی مواقع دمای هوا را زیر صفر درجه و در موارد دیگر دمای هوا را صفر درجه یا بالای صفر درجه اعلام میکند. دمای هوای زیر صفر درجه با اعدادی مثل ۵-، ۱۰-، ۱۸- و غیره بیان میشود اما دمای هوای بالای صفر درجه را بدون علامت – بیان میکنند. بهطور کلی، در ریاضی اعداد بالای صفر را با علامت + و اعداد زیر صفر را با علامت – نشان میدهند. در این مقاله، قرار است شما را با دنیای جدیدی از اعداد بهنام اعداد صحیح آشنا کنیم. ابتدا به شما میگوییم که اعداد صحیح چه اعدادی هستند و چه ویژگیهایی دارند. سپس، عملیات ریاضی برای عدد صحیح را با حل مثال آموزش میدهیم.
عدد صحیح چیست؟
عدد صحیح عددی کامل و بدون بخش کسری یا اعشاری است که اعداد منفی و مثبت و همچنین عدد صفر را شامل میشود. اعداد بالای صفر یا بیشتر از آن را اعداد مثبت و اعداد پایین صفر یا کمتر از آن را اعداد منفی میگویند. اعدادی مانند ۱، ۲۳، ۱۳۶ و مانند آن اعداد مثبت و اعدادی مانند ۳-، ۴۵-، ۹۹- و غیره اعداد منفی هستند.

اولین نفری باشید که از اخبار و اطلاعیههای مرتبط با پایه تحصیلیتان باخبر میشود!
مجموعه اعداد صحیح
مجموعه اعداد صحیح را با حرف Z و بهصورت زیر نمایش میدهند:
Z = {…,-۵,-۴,-۳,-۲,-۱,۰,۱,۲,۳,۴,۵,…}
برای درک تعریف اعداد صحیح به شکل زیر توجه کنید. همانطور که میبینید، اعداد حسابی و اعداد طبیعی زیرمجموعه اعداد صحیح هستند.
پیشنهاد مطالعه: مجموعه اعداد چیست؟

نمایش اعداد صحیح روی محور مختصات
اگر بخواهیم اعداد صحیح را روی محور مختصات نشان دهیم، مانند شکل زیر، عدد صفر را در وسط محور، اعداد صحیح مثبت را در سمت راست صفر و اعداد صحیح منفی را در سمت چپ صفر قرار میدهیم. هرچه از سمت چپ بهسمت راست محور حرکت کنیم، اعداد بزرگتر میشوند و بالعکس، هرچه از سمت راست بهسمت چپ پیش برویم، اعداد کوچکتر خواهند شد. برای مثال، عدد ۶+ از عدد ۶- بزرگتر است.
نکته: اعداد صحیح مثبت را میتوان بدون علامت + نوشت. مثلاً میتوانیم بهجای ۷+ بنویسیم ۷.
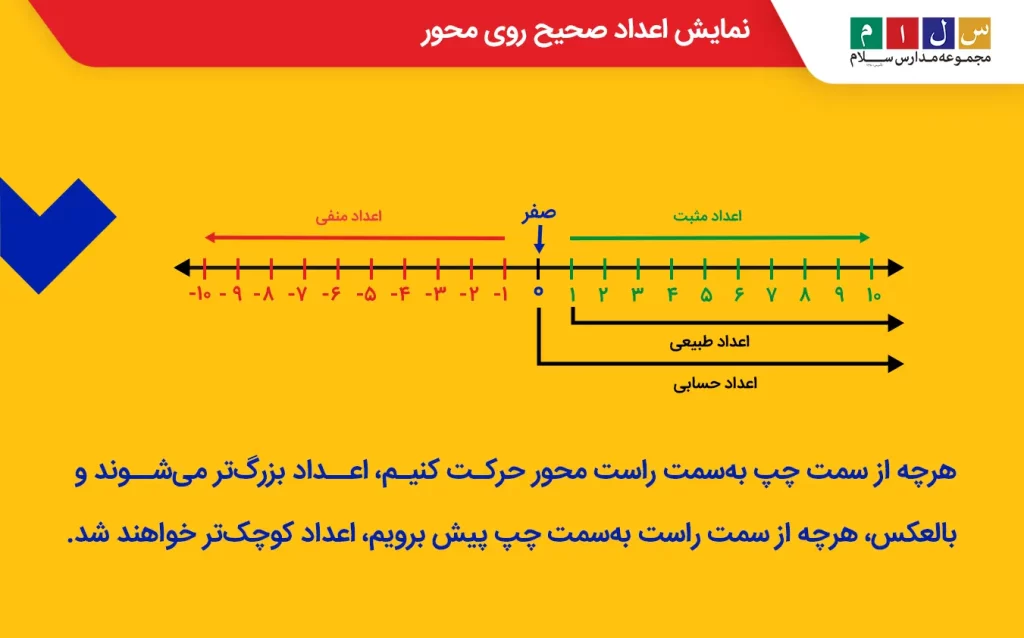
با توجه به محور بالا، میتوان نکات زیر را بیان کرد:
- هرچه مقدار عدد مثبت بیشتر میشود، آن عدد بزرگتر خواهد بود. مثلاً عدد ۱۵+ از ۱۲+ بزرگتر است.
- هرچه مقدار عدد منفی بیشتر میشود، آن عدد کوچکتر است. برای مثال، عدد ۳۳- از ۱۹- کوچکتر است.
- همه اعداد مثبت بزرگتر از اعداد منفی هستند. بهعنوان مثال، عدد ۱۷+ بزرگتر از ۲۰- است.
- اعداد منفی و اعداد مثبت قریته یکدیگر هستند. مثلاً عدد ۵- قرینه ۵+ و بالعکس عدد ۵+ نیز قرینه ۵- است.
لیست اعداد اول 1 تا 100را ببینید و روش پیدا کردن آنها را یاد بگیرید.
چهار عمل اصلی ریاضی در اعداد صحیح
در این قسمت، چهار عمل اصلی جمع، تفریق، ضرب و تقسیم در اعداد صحیح را با مثال توضیح میدهیم.
جمع اعداد صحیح
برای جمع کردن اعداد صحیح باید به علامت آنها توجه کنیم. بهطور کلی، برای جمع اعداد صحیح دو حالت وجود دارد:
- اگر اعداد صحیح همعلامت باشند، عمل جمع را بدون در نظر گرفتن علامت اعداد، انجام داده و سپس، علامت موردنظر را قرار میدهیم. برای مثال، اگر بخواهیم دو عدد صحیح ۳- و ۷- را که هر دو دارای علامت منفی هستند، با هم جمع بزنیم، ابتدا آنها را بدون در نظر گرفتن علامت جمع میکنیم (۱۰=۳+۷). سپس، علامت منفی هر دو عدد یعنی – را کنار آن قرار میدهیم.
۱۰- = (۷-) + (۳-)
- اگر اعداد صحیح همعلامت نباشند، دو عدد را بدون توجه به علامتشان از هم کم میکنیم و سپس، علامت عدد بزرگتر را پشت مقدار بهدستآمده مینویسیم. بهعنوان مثال، برای جمع کردن دو عدد ۶- و ۲+ ابتدا دو عدد ۶ و ۲ را بدون در نظر گرفتن علامت از هم کم میکنیم. با کم کردن این دو عدد از هم مقدار ۴ بهدست میآید. پس از عمل تفریق، علامت عدد بزرگتر یعنی ۶ را که – است در کنار عدد حاصل قرار میدهیم.
۴- = ۲ + ۶-
در جدول زیر، نکات جمع کردن اعداد صحیح را بهصورت خلاصه آوردهایم.
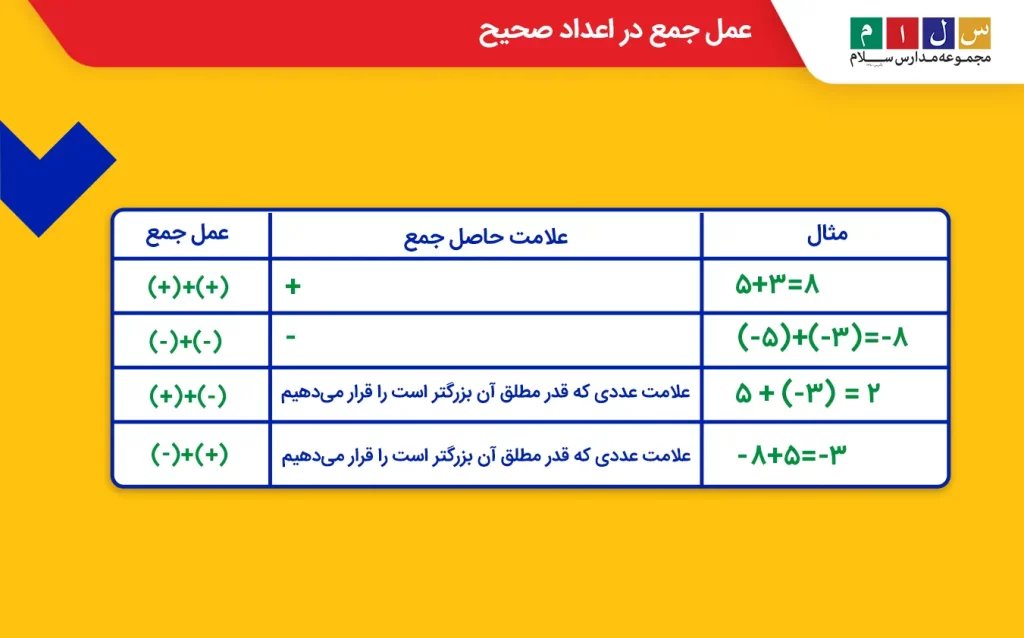
تفریق اعداد صحیح
برای تفریق اعداد صحیح، میتوانیم ابتدا علامت عدد دوم را تغییر دهیم و سپس، عمل تفریق را به عمل جمع تبدیل کنیم. به مثال زیر توجه کنید تا بهتر متوجه شوید:
۱۳- = (۷-) + (۶-) = (۷+) – (۶-)
در این مثال، پس از تغییر علامت عدد دوم (۷+) و تبدیل تفریق به جمع، عمل جمع را با توجه به آنچه گفته شد انجام میدهیم، یعنی دو عدد همعلامت را بدون توجه به علامتشان با هم جمع میکنیم و بعد از آن علامت هر دو عدد را که – است، کنار حاصلجمع قرار میدهیم.
یک مثال دیگر نیز حل میکنیم، اما این بار عدد دوم را یک عدد منفی در نظر میگیریم:
۹+ = (۴+) + (۵+) = (۴-) – (۵+)
همانطور که گفتیم برای تفریق دو عدد صحیح، نخست علامت عدد دوم را تغییر میدهیم. در اینجا عدد دوم ۴- است که با تغییر علامت به ۴+ تبدیل میشود. پس از تغییر علامت عدد دوم، باید علامت تفریق (-) را به علامت جمع (+) تبدیل کنیم و سپس، عمل جمع را انجام دهیم.
جدول زیر، قواعد تفریق اعداد صحیح را بهخوبی نشان میدهد.
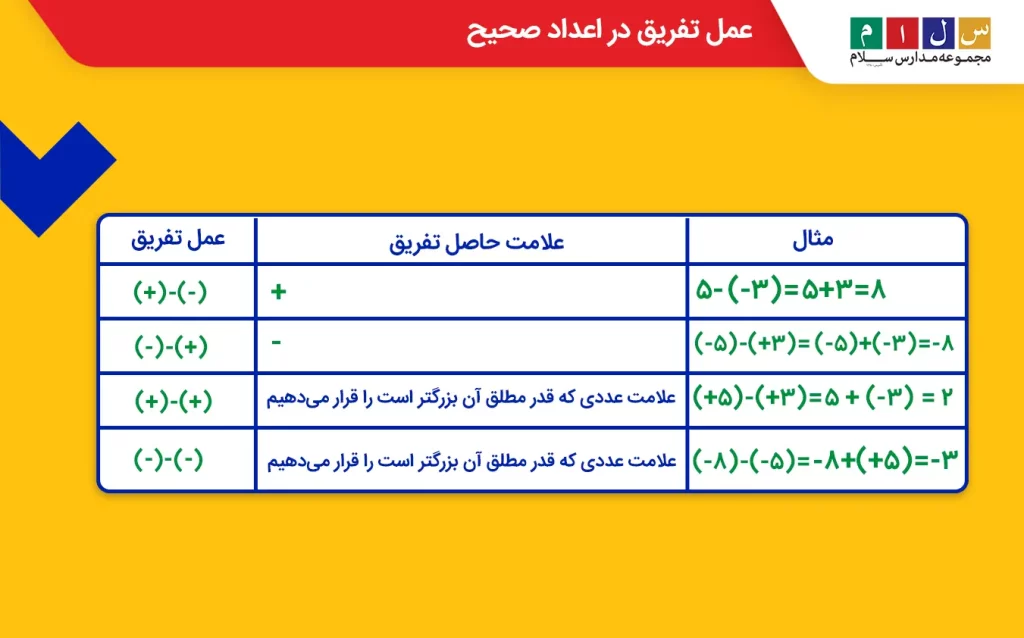
ضرب اعداد صحیح
برای عمل ضرب اعداد صحیح، کافیست اعداد را در هم ضرب کنیم، اما برای تعیین علامت حاصل آن، دو قانون وجود دارد:
- اگر هر دو عدد صحیح همعلامت باشند یعنی هر دو مثبت یا هر دو منفی باشند، علامت حاصلضرب + خواهد بود.
- اگر دو عدد صحیح همعلامت نباشند، حاصلضرب علامت – خواهد داشت.
- جدول زیر، برای هر کدام از این حالتها یک مثال حلشده آورده شده است که میتواند به یادگیری بهتر شما کمک کند.
همچنین در گسترده نویسی، هر عدد صحیح به صورت مجموع ارزشهای مکانیاش نمایش داده میشود. برای مثال، عدد 456 به صورت 6 + 50 + 400 نوشته میشود که کمک میکند در هنگام ضرب، هر بخش از عدد را جداگانه ضرب کرده و سپس نتایج را با توجه به قوانین علامت جمع کنیم.
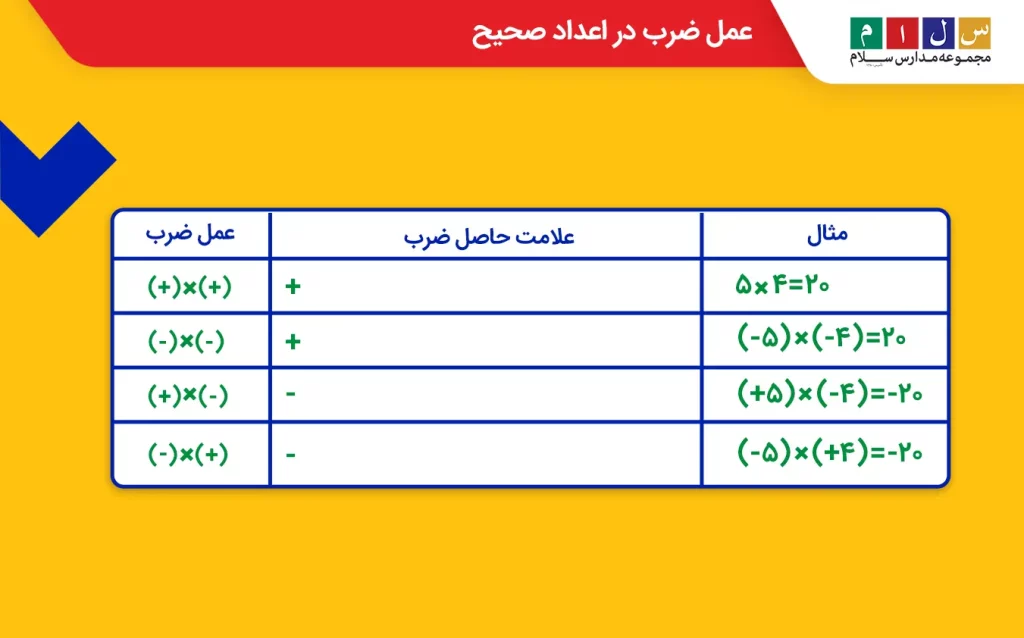
تقسیم اعداد صحیح
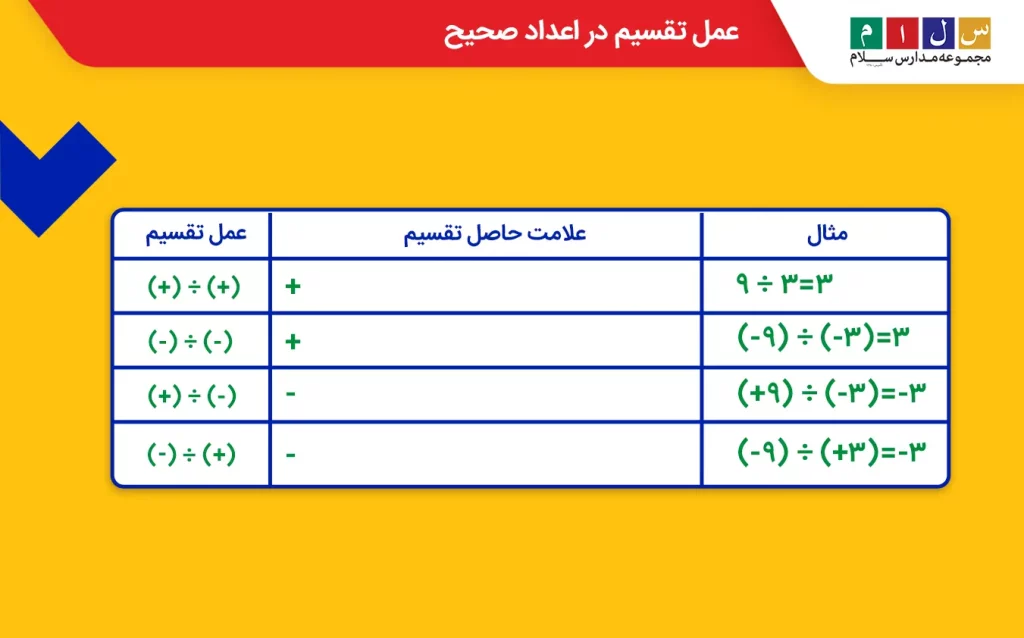
در تقسیم اعداد صحیح، پس از تقسیم اعداد بر یکدیگر، علامت مقدار حاصل را مانند آنچه در عمل ضرب گفتیم، بهصورت زیر تعیین میکنیم:
- اگر اعداد همعلامت بودند، علامت مقدار حاصل را + قرار میدهیم.
- اگر اعداد همعلامت نبودند،علامت مقدار بهدست آمده را – میگذاریم.
عدد مرکب عدد صحیحی است که به غیر از ۱ و خودش، بر اعداد دیگری نیز بخشپذیر است، مانند ۸ که علاوه بر ۱ و ۸، بر ۲ و ۴ هم بخشپذیر است. در جدولی که در زیر آمده است، چند مثال از تقسیم اعداد صحیح حل کردهایم.
ویژگی های اعداد صحیح
در این بخش، ویژگیهای اعداد صحیح را توضیح میدهیم و برای هر کدام مثال میزنیم.
خاصیت بسته بودن
اعداد صحیح نسبت به سه عمل جمع، تفریق و ضرب بسته هستند. این بدین معنی است که حاصل جمع، تفریق و ضرب دو عدد صحیح حتماً یک عدد صحیح خواهد بود. مثالهای زیر، این ویژگی را بهخوبی نشان میدهند.
-۵ + ۴ = -۱
۸ – ۵ = ۳
۲ × ۳ = ۶
در عمل تقسیم ممکن است مانند مثال زیر حاصل تقسیم یک عدد غیرصحیح باشد:
۱۵ ÷ ۲= ۷.۵
خاصیت جابجایی
این ویژگی بیان میکند که جابهجا کردن اعداد صحیح در عمل جمع و ضرب، مقدار حاصل را تغییر نخواهد داد. توجه داشته باشید که این ویژگی فقط برای عمل جمع و ضرب صدق میکند، اما در تفریق و تقسیم اینگونه نیست. خاصیت جابهجایی در مثالهای زیر نشان داده شده است.
-۵+۲=۲+-۵=-۳
۳ × ۶ = ۶ × ۳ = ۱۸
خاصیت شرکت پذیری
با توجه به این ویژگی، تغییر گروهبندی اعداد صحیح برای عملیات ریاضی جمع و ضرب، تغییری در جواب بهدستآمده ایجاد نمیکند. بهطور کلی، اگر a، b و c اعداد صحیح باشند، داریم:
( a + (b + c) = a + (b + c
( a × ( b + c ) = a × (b × c
خاصیت توزیعی
منظور از خاصیت توزیعی این است که در اعداد صحیح میتوانیم برای محاسبات راحتتر، ضرب چند عدد صحیح را بهصورت گستردهتر بنویسیم. برای مثال، اگر a، b و c اعداد صحیح باشند، طبق خاصیت توزیعی خواهیم داشت:
( a ×( b + c ) = ( a × b ) + ( a × c
مثال زیر، این ویژگی را بهخوبی نشان میدهد.
-۲ × ۶ + ۱= -۲ × ۶ + -۲ × ۱ = -۱۴
خاصیت معکوس جمعی
طبق این ویژگی، حاصلجمع یک عدد صحیح و مقدار منفی آن (قرینه آن) همواره صفر خواهد بود.
۱۵ + ( -۱۵ ) = 0
خاصیت معکوس ضربی
این ویژگی بیان میکند که حاصلضرب یک عدد صحیح در معکوس آن برابر با یک است.
خاصیت همانی
براساس این ویژگی، هر عدد صحیحی که به صفر اضافه شود، حاصل، همان عدد صحیح خواهد بود. همچنین، هر عدد صحیحی که در یک ضرب شود، همان عدد صحیح را بهدست میدهد.
۱۰+۰=۰+۱۰=۱۰
۱۰×۱=۱×۱۰=۱۰
پیشنهاد مطالعه اعداد اعشاری و عملیات ریاضی در آنها
سخن پایانی
اعداد صحیح اعدادی شامل اعداد منفی، مثبت و صفر هستند. اعداد مثبت قرینه اعداد منفی هستند و از اعداد منفی بزرگترند. عدد صحیح بخش کسری و اعشاری ندارد. اگر بخواهیم این اعداد را روی محور نشان دهیم، عدد صفر را وسط محور، اعداد مثبت را سمت راست صفر و اعداد منفی را سمت چپ صفر قرار میدهیم. در محور اعداد صحیح، هرچه بهسمت راست میرویم، اعداد بزرگتر و هرچه بهسمت چپ میرویم اعداد کوچکتر میشوند که این مسئله را به صورت کامل در مقاله ارزش مکانی اعداد و جدول ارزش مکانی توضیح دادهایم. در اعداد صحیح نیز مانند سایر اعداد میتوان چهار عمل اصلی ریاضی یعنی جمع، تفریق، ضرب و تقسیم را انجام داد که در این مقاله همراه با مثال درمورد هر یک از آنها مفصل توضیح دادهایم. پیشنهاد میکنیم برای یادگیری عمیقتر، تمرینها و مثالهای بیشتری دراینباره حل کنید.
سؤالات متداول
- اعداد صحیح چیست؟
اعداد صحیح اعداد کاملی هستند که بخش اعشاری و کسری ندارند. - مجموعه اعداد صحیح شامل چه اعدادی است؟
مجموعه اعداد صحیح متشکل از عدد صفر، اعداد مثبت و اعداد منفی است. - اعداد صحیح مثبت و اعداد صحیح منفی چه تفاوتی دارند؟
اعداد صحیح مثبت اعداد بزرگتر از صفر و اعداد صحیح منفی اعداد کوچکتر از صفر هستند. اعداد مثبت را با علامت + و اعداد منفی را با علامت – نشان میدهند. - خاصیت معکوس جمعی اعداد صحیح چیست؟
معکوس جمعی هر عدد صحیح a، عدد a− است که مجموع آنها صفر میشود.









