فهرست مطالب
Toggleمفهوم تقارن یکی از جذابترین مفاهیم در هندسه است که زیبایی خاصی به اشکال مختلف میبخشد. بارزترین تقارنی که هر یک از ما روزانه آن را مشاهده میکنیم، تقارن چهره و یکسان بودن سمت راست و چپ صورت انسان است. البته، نمونههای تقارن در طبیعت و در دنیای پیرامون ما بهوفور یافت میشود، مانند تقارن برگ درختان و گلها، طرح روی بدن حیوانات و حتی بسیاری از لوازم منزل مانند فرشها و قالیچهها.
جالب است بدانید که تقارن انواع مختلفی دارد و محدود به یک نوع نیست. برای همین در این مقاله قصد داریم شما را با انواع تقارن آشنا کرده و با آوردن مثالهای تصویری برای هر کدام به درک بهتر شما از این مفهوم کمک کنیم.
تقارن چیست؟
در ریاضیات، اگر بتوان یک شکل را به دو نیمه یکسان و مشابه تقسیم کرد، طوری که یک نیمه قرینه و بازتاب نیمه دیگر باشد، آن شکل دارای تقارن یا بهعبارتی متقارن مینامند اما چون تقارن انواع گوناگونی دارد، تعریف کاملتری میتوان برای آن ارائه کرد.
بهطور کلی، مفهوم تقارن به یکسان بودن یک شکل با شکل دیگر و منطبق شدن روی آن پس از جابهجایی یا دوران اشاره دارد. شکلهایی که در تصویر زیر میبینید، همگی نمونههایی از تقارن هستند.
پیشنهاد مطالعه: تقارن چیست؟
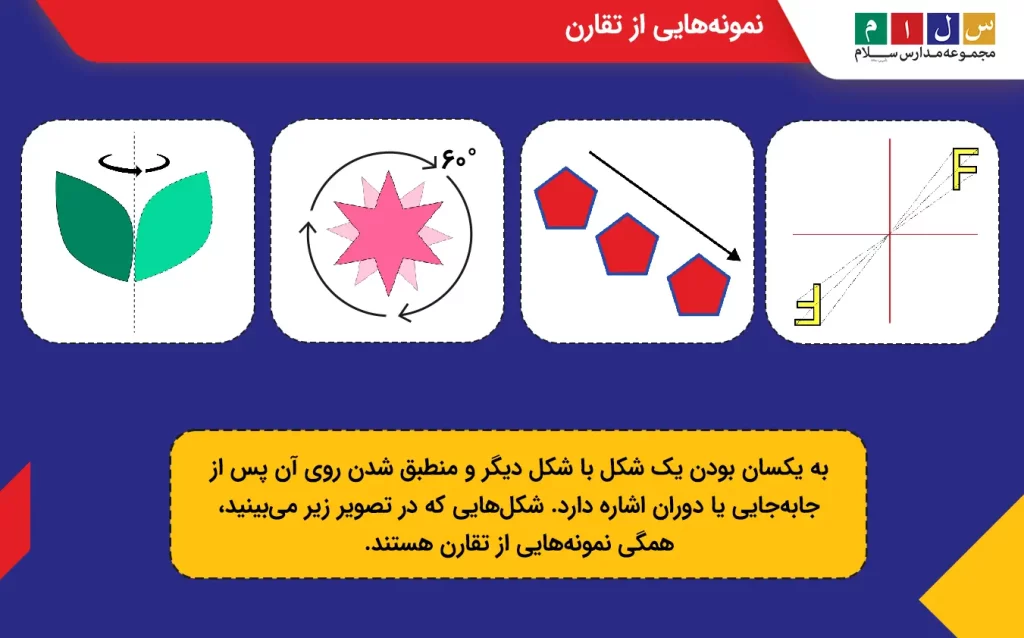
اولین نفری باشید که از اخبار و اطلاعیههای مرتبط با پایه تحصیلیتان باخبر میشود!
انواع تقارن چیست؟
ازآنجا که شناخت انواع تقارن به شما کمک میکند تا الگوها و ساختارهای پیرامون خود را بهتر درک کنید، این بخش را به معرفی سه نوع از مهمترین انواع تقارن اختصاص میدهیم.
تقارن محوری
تقارن محوری که نام دیگر آن تقارن بازتابی یا آینهای است، نوعی تقارن است که در آن نیمی از شکل، مشابه و مساوی با نیمه دیگر است. برای اینکه تعیین کنیم آیا یک شکل دارای تقارن محوری است یا خیر، کافیست مانند شکل زیر از خطی فرضی آن را تا کنیم، اگر دو نیمه شکل از خط تا روی هم منطبق شدند و کاملاً یکدیگر را پوشاندند، آن شکل تقارن محوری خواهد داشت و بهعبارت دیگر، نسبت به خط فرضی متقارن خواهد بود.

خط تقارن
خط تقارن یا محور تقارن خطی فرضی است که یک شکل را به دو نیمه یکسان و مشابه تقسیم میکند، طوری که اگر از این خط شکل را تا کنیم، دو نیمه آن روی هم منطبق میشوند. یک شکل بسته با ظاهری که دارد میتواند یک یا چند خط تقارن داشته باشد.
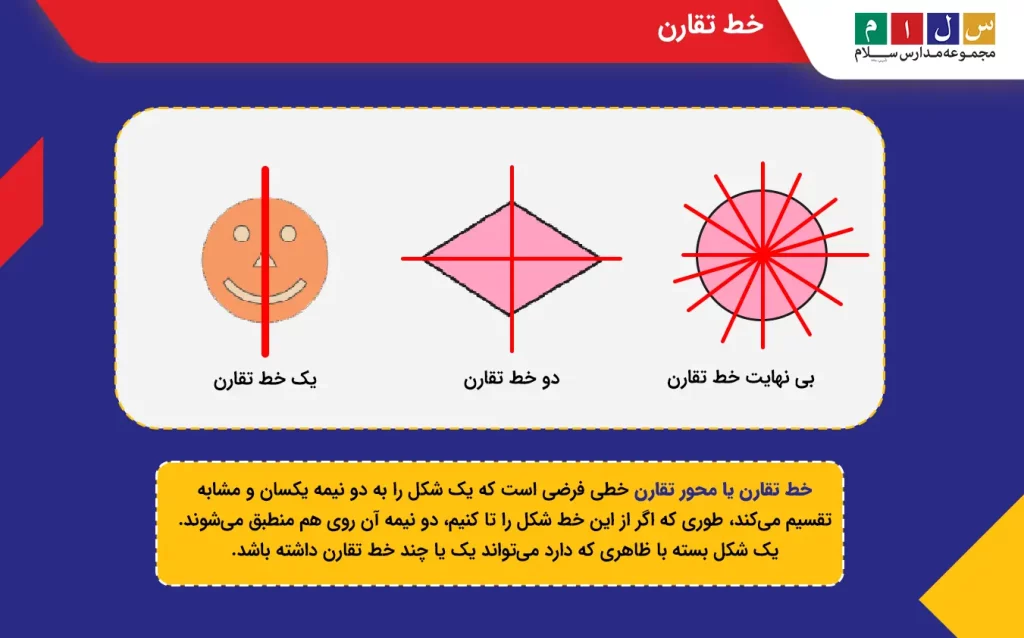
اگر مایل هستید درمورد خط تقارن بیشتر بدانید، مطالعه مقاله خط تقارن را به شما پیشنهاد میکنیم. در آنجا بهطور مفصل، درمورد تعداد خطوط تقارن هر کدام از اشکال هندسی صحبت کردهایم.
انواع خط تقارن
خطوط تقارن از نظر نوع جهتگیری به سه دسته طبقهبندی میشوند:
- خط تقارن افقی: خطی افقی که شکل متقارن را به دو قسمت مساوی بالا و پایین تقسیم میکند.
- خط تقارن عمودی: خطی عمودی که شکل متقارن را به دو قسمت مساوی چپ و راست تقسیم میکند.
خط تقارن مورب: خطی مورب که شکل متقارن را بهصورت مورب به دو قسمت مساوی تقسیم میکند.

مثال ۱: شکل زیر چند محور تقارن دارد؟ نوع خط تقارن را مشخص کنید.
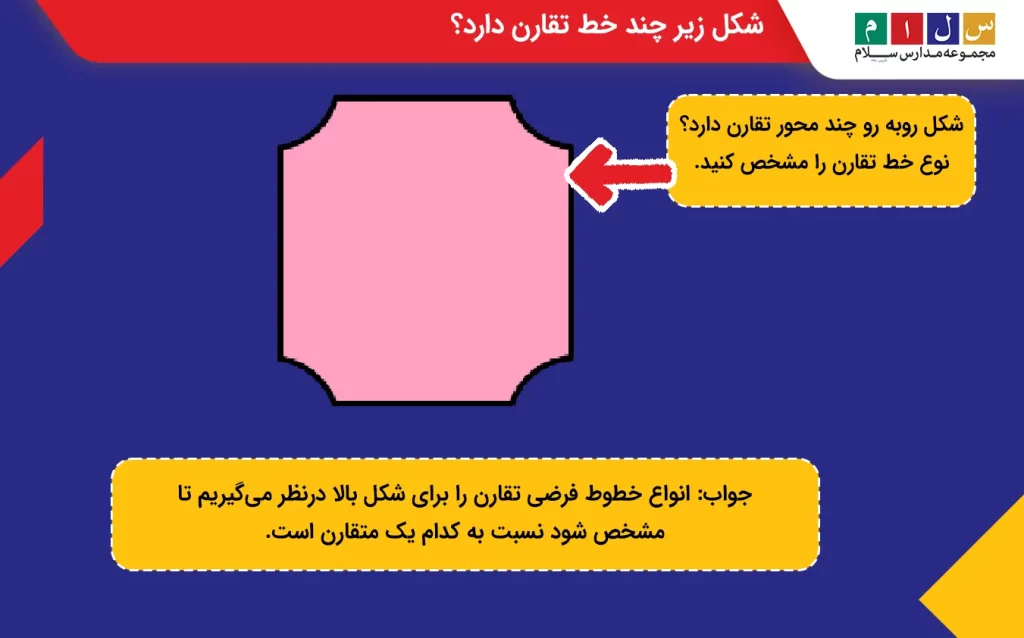
جواب: انواع خطوط فرضی تقارن را برای شکل بالا درنظر میگیریم تا مشخص شود نسبت به کدام یک متقارن است.

همانطور که در شکل بالا نشان داده شده است، این شکل، یک خط تقارن افقی، یک خط تقارن عمودی و دو خط تقارن مورب دارد.
مثال ۲: آیا شکل زیر نسبت به خط نشانداده شده متقارن است؟

جواب: خیر. زیرا اگر مانند شکل زیر، خط دادهشده را خط تا درنظر بگیریم، اجزای دو سیب دقیقاً روی هم منطبق نمیشوند. برای مثال، برگهای دو سیب کاملاً روی هم قرار نمیگیرند. درنتیجه، این خط، خط تقارن نیست.

مثال ۳: آیا شکل زیر متقارن است؟

جواب: خیر، شکل بالا متقارن نیست، زیرا همانطور که در شکل زیر میبینید، با رسم خطوط فرضی مختلف نمیتوان آن را به دو نیمه یکسان تقسیم کرد.

تقارن چرخشی
اگر یک شکل پس از چرخش با زاویه مشخص حول یک نقطه، به حالت اولیهاش بازگردد و روی خودش منطبق شود، آن شکل دارای تقارن چرخشی خواهد بود. کوچکترین و اولین زاویهای که شکل پس از دوران با آن مقدار روی خودش منطبق میشود را زاویه چرخش و تعداد دفعاتی که شکل پس از چرخش ۳۶۰ درجه روی خودش منطبق میشود را مرتبه تقارن چرخشی میگویند. برای یادگیری بهتر و کاملتر مفهوم هندسی زاویه پیشنهاد میکنیم مقاله زاویه چیست را مطالعه کنید.
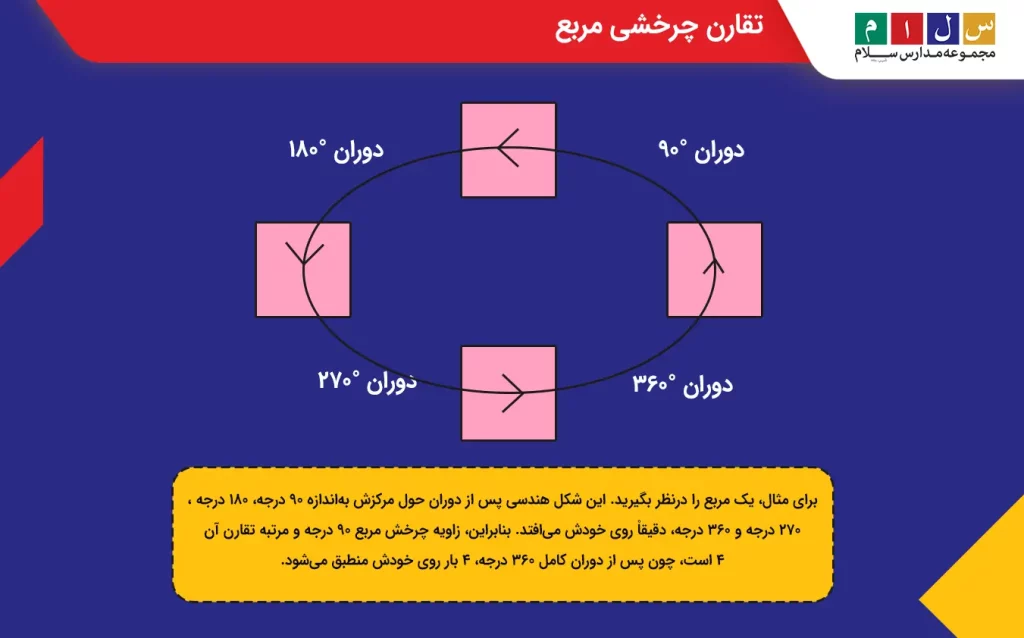
برای مثال، یک مربع را درنظر بگیرید. این شکل هندسی پس از دوران حول مرکزش بهاندازه ۹۰ درجه، ۱۸۰ درجه ، ۲۷۰ درجه و ۳۶۰ درجه، دقیقاْ روی خودش میافتد. بنابراین، زاویه چرخش مربع ۹۰ درجه و مرتبه تقارن آن ۴ است، چون پس از دوران کامل ۳۶۰ درجه، ۴ بار روی خودش منطبق میشود.
پیشنهد مطالعه: اندازه گیری زاویه با نقاله و گونیا
مثال ۱: تقارن چرخشی شکل زیر را حول نقطه داده شده بررسی کنید.
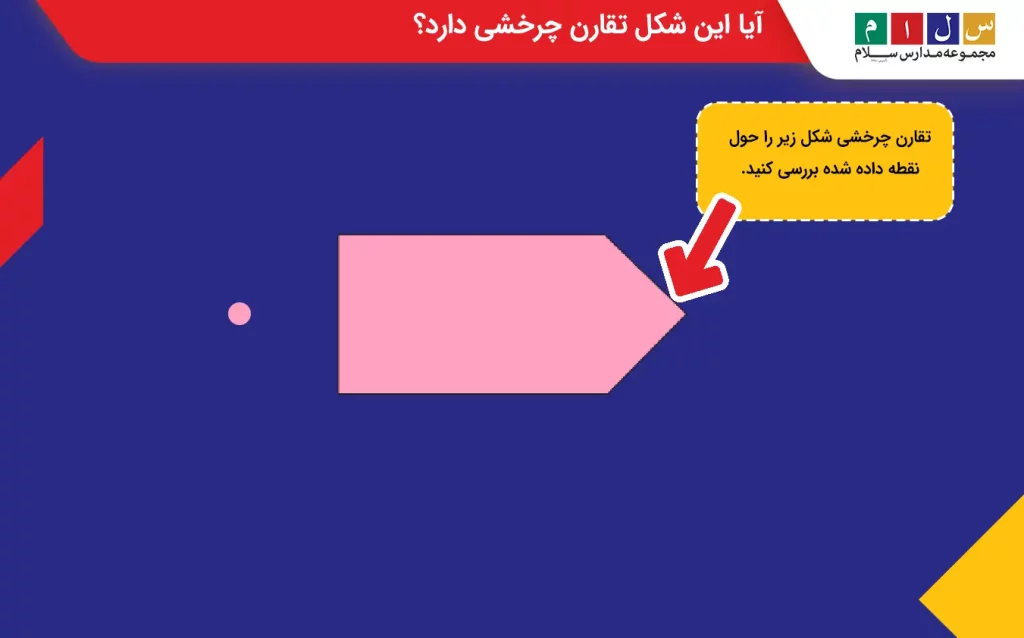
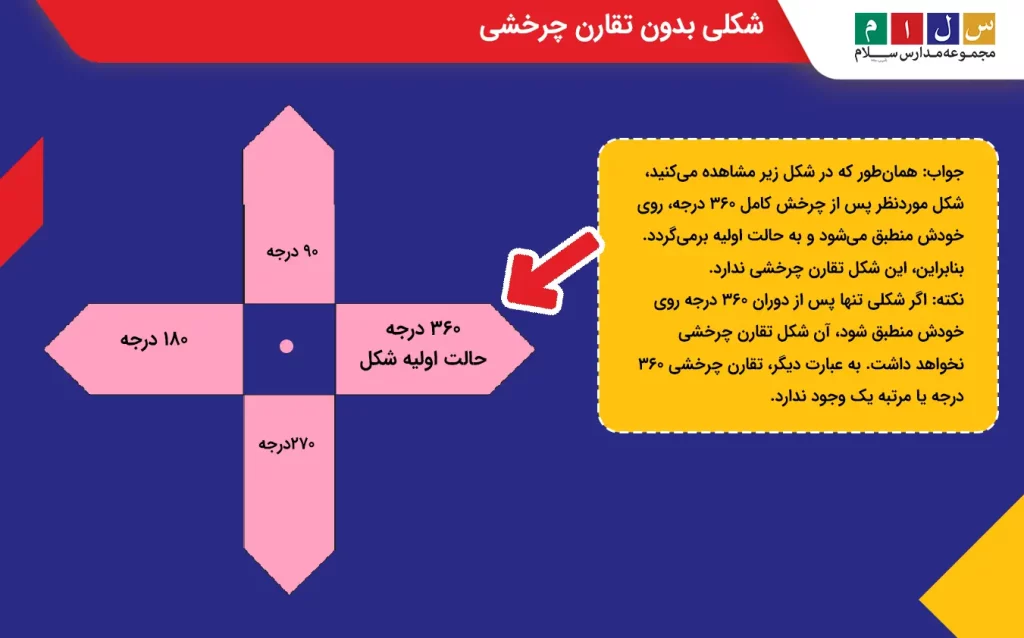
جواب: همانطور که در شکل زیر مشاهده میکنید، شکل موردنظر پس از چرخش کامل ۳۶۰ درجه، روی خودش منطبق میشود و به حالت اولیه برمیگردد. بنابراین، این شکل تقارن چرخشی ندارد.
نکته: اگر شکلی تنها پس از دوران ۳۶۰ درجه روی خودش منطبق شود، آن شکل تقارن چرخشی نخواهد داشت. به عبارت دیگر، تقارن چرخشی ۳۶۰ درجه یا مرتبه یک وجود ندارد.
مثال ۲: مرتبه تقارن چرخشی یک ستاره پنجرأس را حول نقطه مرکزی اش تعیین کنید.
جواب: ستاره پنجرأس زوایا و اضلاع مساوی دارد. ازآنجا که این ستاره دارای پنج رأس با فاصله مساوی است، میتوان گفت ستاره موردنظر اولین بار پس از دوران ۷۲ درجه به حالت اولیهاش برمیگردد (۳۶۰ را بر ۵ تقسیم کنید). درنتیجه، در یک دوران کامل۳۶۰ درجه، ستاره پنج بار روی خودش منطبق میشود. بنابراین، زاویه چرخش ستاره پنجرأس ۷۲ درجه و مرتبه تقارن آن ۵ خواهد بود.

تقارن مرکزی
اگر یک شکل را بهاندازه نیمدور (۱۸۰ درجه) حول یک نقطه مرکزی بچرخانیم، طوری که پس از چرخش، شکل روی خودش منطبق شود، آن شکل دارای تقارن مرکزی یا تقارن نقطهای خواهد بود. تقارن مرکزی نوعی تقارن چرخشی مرتبه دو است، یعنی شکل در یک دوران کامل دو بار روی خودش منطبق میشود؛ بار اول در چرخش ۱۸۰ درجه و بار دوم در دوران ۳۶۰ درجه. برای مثال، شکل زیر نسبت به مبدأ، تقارن مرکزی و بهعبارت دیگر، تقارن چرخشی مرتبه دو دارد.
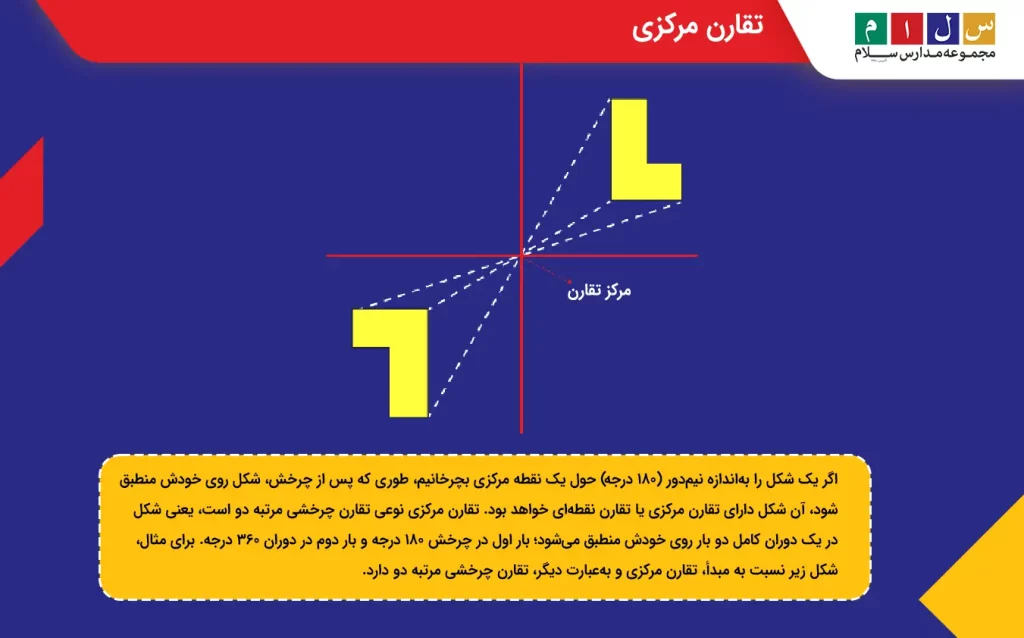
مرکز تقارن
مرکز تقارن نقطهای است که اگر یک شکل را حول آن بهاندازه نیمدور (۱۸۰ درجه) بچرخانیم، روی خودش منطبق میشود و به حالت اولیهاش برمیگردد. در شکل بالا، مرکز تقارن نشان داده شده است.
برای تشخیص اینکه آیا یک شکل تقارن مرکزی دارد یا خیر، میتوان از دو روش استفاده کرد:
- شکل را ۱۸۰ درجه حول مرکز بچرخانید. اگر شکل پس از چرخش روی خودش منطبق شد، یعنی شکل موردنظر تقارن مرکزی دارد.
- نقاط مشابه را مانند شکل بالا به مرکز وصل کنید. اگر فاصله نقاط مشابه در دو طرف تا مرکز یکسان بود، یعنی آن شکل دارای تقارن مرکزی است.
مثال ۱: تقارن مرکزی شکل زیر را حول مبدأ بررسی کنید.
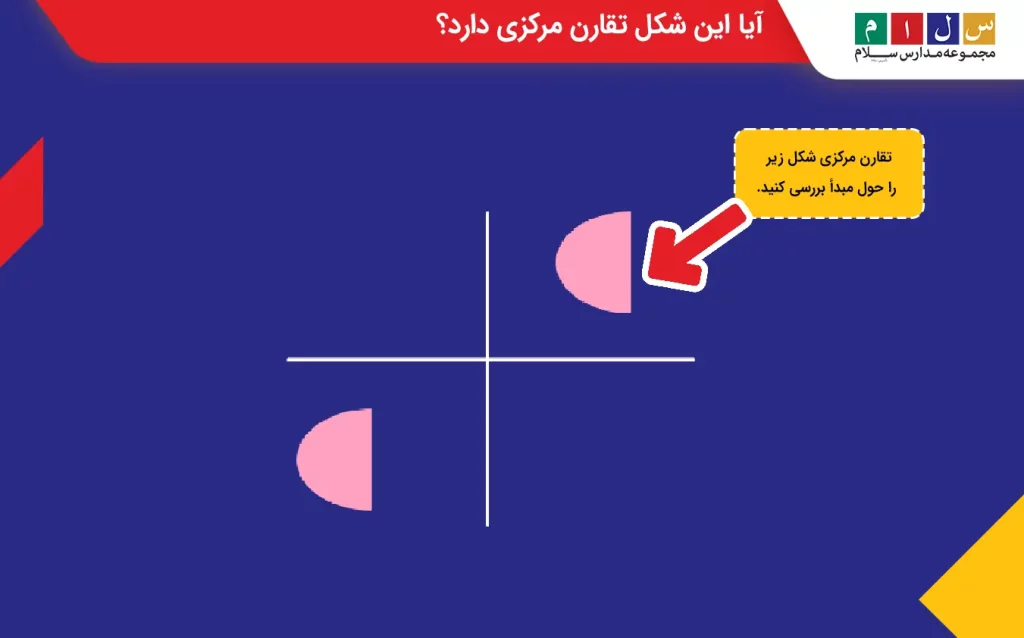
جواب: اگر شکل را نیمدور حول مبدأ بچرخانیم، روی شکل دیگر منطبق نمیشود. از طرفی، اگر مانند آنچه در شکل زیر نشان داده شده است، نقاط مشابه را به مرکز وصل کنیم، مشخص میشود که فاصله آنها تا مرکز برابر نیست.

مثال ۲: آیا شکل هندسی زیر نسبت به مرکزش متقارن است؟
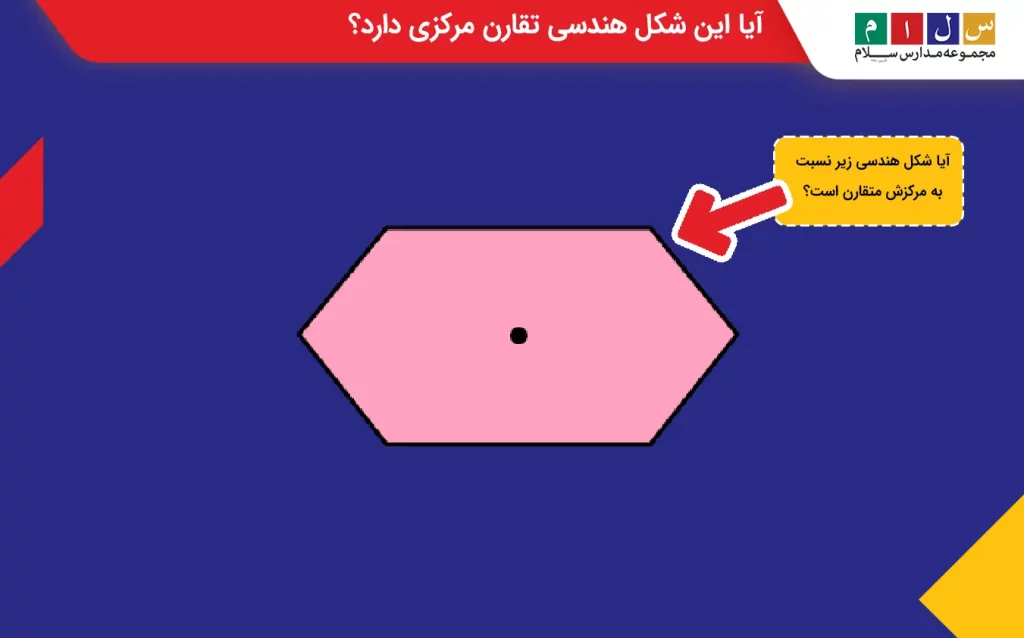
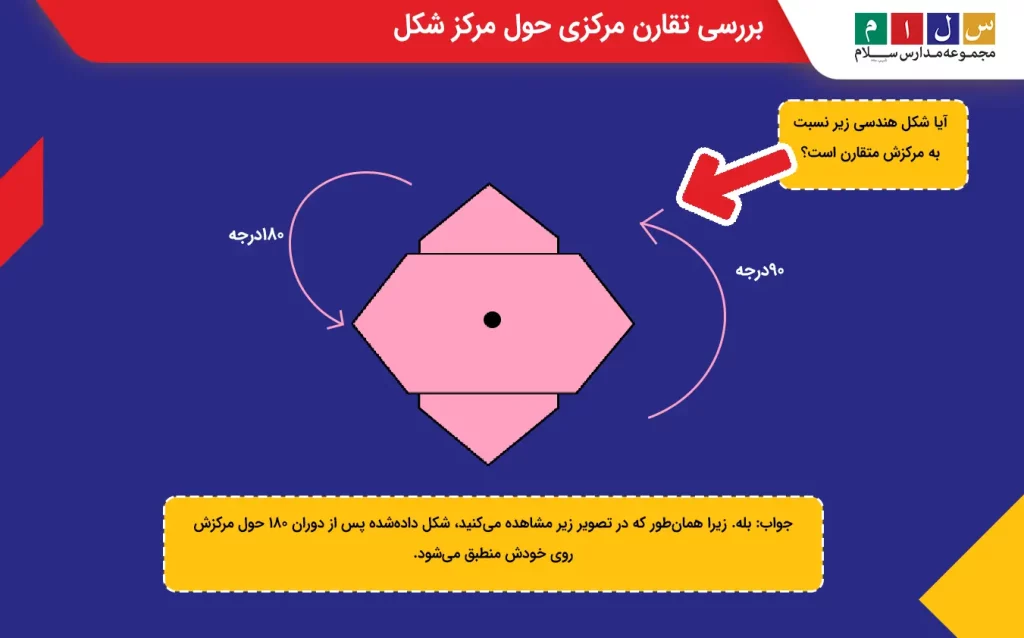
جواب: بله. زیرا همانطور که در تصویر زیر مشاهده میکنید، شکل دادهشده پس از دوران ۱۸۰ حول مرکزش روی خودش منطبق میشود.
سخن پایانی
مفهوم تقارن به یکسان بودن یک شکل با شکل دیگر و منطبق شدن روی آن پس از جابهجایی یا دوران اشاره دارد. این مفهوم هندسی انواع مختلفی دارد که عبارتاند از: تقارن محوری، تقارن چرخشی و تقارن مرکزی.
۱) اگر یک شکل به دو نیمه مساوی تقسیم شود، طوری که اگر آن شکل از یک خط فرضی تا شود، دو نیمه کاملاً روی هم منطبق شوند، شکل موردنظر دارای تقارن محوری خواهد بود. خطی که شکل را به دو قسمت یکسان و مشابه تقسیم میکند، خط تقارن نام دارد.
۲) اگر یک شکل پس از دوران با اندازه مشخص حول یک نقطه، روی خودش منطبق شود، شکل تقارن چرخشی خواهد داشت.
۳) اگر شکل پس از چرخش ۱۸۰ درجه حول یک نقطه به حالت اولیه خود برگردد، میگوییم آن شکل دارای تقارن مرکزی است. به نقطهای که شکل نسبت به آن تقارن مرکزی دارد، مرکز تقارن میگویند.
سؤالات متداول
- تقارن یعنی چه؟
به یکسان بودن یک شکل با شکلی دیگر پس از جابهجایی یا چرخش تقارن میگویند. - انواع تقارن را نام ببرید.
انواع تقارن عبارتاند از تقارن محوری، تقارن چرخشی و تقارن مرکزی. - تقارن محوری چیست؟
یکی از انواع تقارن است که در آن نیمه یک شکل بازتاب نیمه دیگر است. - خط تقارن چیست؟
خطی است که یک شکل را به دو نیمه مساوی و مشابه تقسیم میکند. - تقارن چرخشی چیست؟
نوعی تقارن است که در آن شکل پس از چرخش بهاندازه معین حول یک نقطه، به حالت اولیه خود بازمیگردد. - تقارن مرکزی چیست؟
در این نوع تقارن که نوعی تقارن چرخشی است، شکل پس از چرخش بهاندازه نیمدور (۱۸۰ درجه) حول یک نقطه مرکزی، روی خودش منطبق میشود.









