در مقاله مساحت چیست گفتیم که به اندازه سطح داخلی یک شکل بسته، مساحت آن می‌گویند. در مقاله مساحت مثلث کمی جزئی‌نگرتر شدیم و به بررسی فرمول‌ها و روش‌های محاسبه مساحت انواع مثلث از جمله مثلث قائم‌الزاویه پرداختیم. حالا و در این مقاله قرار است مساحت مثلث قائم الزاویه را با جزئیات کامل و مثال‌های فراوان بررسی کنیم و یک گام دیگر به سمت تکمیل مبحث محیط و مساحت اشکال هندسی برداریم. در اینجا ابتدا به ویژگی‌های اصلی مثلث قائم‌الزاویه اشاره‌ای می‌کنیم و سپس به سراغ توضیح مفهومی، فرمول و روش محاسبه مساحت مثلث قائم‌الزاویه می‌رویم.
مثلث قائم الزاویه چیست و چه انواعی دارد؟
مثلثهای دارای یک زاویه ۹۰ درجه را مثلث قائم‌الزاویه می‌نامند. زاویه قائم (۹۰ درجه) مثلث را معمولا با مربع کوچکی در گوشه آن به تصویر می‌کشند.
مثلثهای قائم‌الزاویه ۲ نوع هستند:
- مثلث قائم‌الزاویه متساوی‌الساقین: این نوع مثلث دارای ۲ زاویه ۴۵ درجه و ۲ ضلع مساوی است:
مثلث قائم‌الزاویه مختلف‌الاضلاع: هیچ‌کدام از ۳ ضلع و ۳ زاویه این نوع مثلث با هم برابر نیستند.
در مثلثهای متساوی‌الساقین به ضلع مقابل زاویه قائمه وتر می‌گویند. این ضلع در تمام مثلثهای قائم‌الزاویه بزرگ‌تر از ۲ ضلع دیگر است. طبق قاعده فیثاغورس، بین وتر (ضلع مقابل زاویه قائمه) و اضلاع مجاور زاویه قائمه رابطه زیر برقرار است:
- c: وتر مثلث قائم‌الزاویه
- a و b: ضلع‌های مجاور زاویه قائمه
پیشنهاد مطالعه: نحوه محاسبه مساحت مثلث متساوی الساقین با مثال
مساحت مثلث قائم الزاویه | تعریف مفهومی
یک مستطیل را تصور کنید، چرا مستطیل؟ چون مستطیل دقیقا از ۲ مثلث قائم‌الزاویه تشکیل شده است:
در مقاله مساحت مستطیل گفتیم که مساحت این شکل هندسی از طریق ضرب طول در عرض محاسبه می‌شود. پس تا اینجا به ۲ نکته رسیدیم:
- مساحت مثلث قائم‌الزاویه نصف مساحت مستطیل است.
- مساحت مستطیل از طریق طول ضربدر عرض محاسبه می‌شود.
از کنار هم گذاشتن ۲ مقدمه بالا به این نتیجه می‌رسیم که مساحت مثلث قائم‌الزاویه از ضرب قاعده در ارتفاع تقسیم بر ۲ حاصل می‌شود. دقت کنید که طول و عرض مستطیل، حکم قاعده و ارتفاع مثلث قائم‌الزاویه را دارند.
فرمول مساحت مثلث قائم الزاویه
برای محاسبه مساحت مثلث قائم‌الزاویه از فرمول اصلی مساحت مثلث استفاده می‌شود:
۲ ÷ (ارتفاع × قاعده) = مساحت مثلث قائم‌الزاویه
چون قاعده و ارتفاع در مثلث قائم‌الزاویه، همان ۲ ضلع مجاور زاویه قائمه هستند، فرمول مساحت مثلث قائم‌الزاویه را می‌توان به این صورت بازنویسی کرد:
۲ ÷ ضرب اضلاع مجاور زاویه قائمه در یکدیگر = مساحت مثلث قائم‌الزاویه
فرمول مساحت مثلث قائم‌الزاویه با عبارت‌های جبری ریاضی به این صورت نوشته می‌شود:
A= (h × b ) ÷ ۲
یا
A = h × b ÷ ۲
مثال: قاعده و ارتفاع یک مثلث قائم‌الزاویه ۳ و ۴ سانتی‌متر هستند. مساحت این مثلث را محاسبه کنید.جواب: چونقاعده و ارتفاع مثلث را داریم، به‌راحتی و از طریق فرمول اصلی مساحت مثلث، جواب را به دست می‌آوریم:
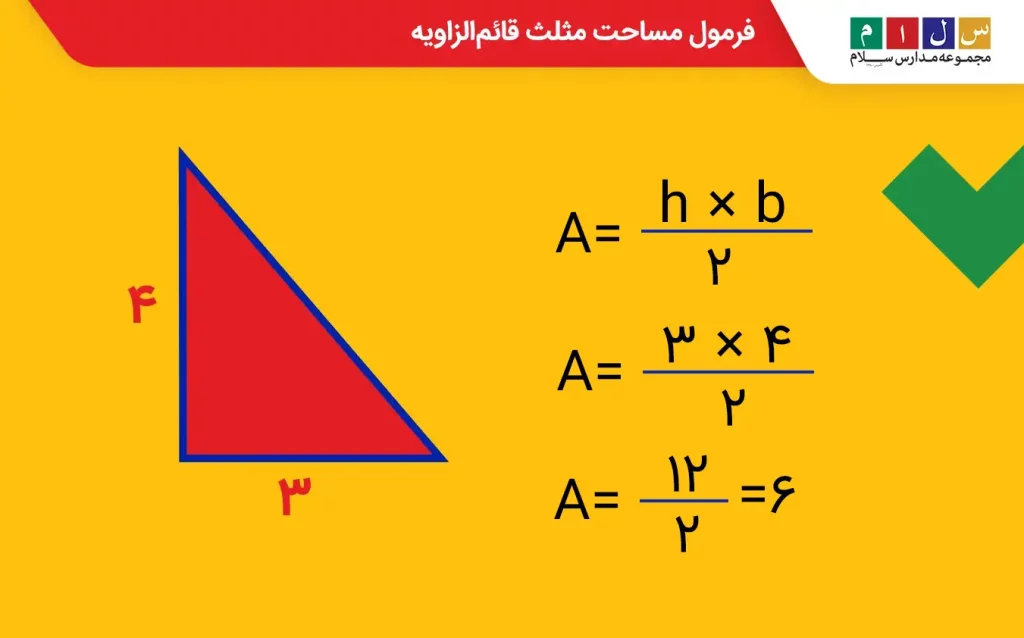
A= (h × b ) ÷ ۲
A= (۴ × ۳ ) ÷ ۲
۳/۵ =۲ ÷ A= ۷
محاسبه مساحت مثلث قائم الزاویه به روش های مختلف
مساحت مثلث قائم‌الزاویه از روش‌های زیادی قابل محاسبه است که در ادامه مهم‌ترین آن‌ها را با هم بررسی می‌کنیم:
- فرمول اصلی مساحت مثلث قائم‌الزاویه
- محاسبه مساحت مثلث قائم‌الزاویه با وتر
- فرمول هرون برای محاسبه مساحت مثلث قائم‌الزاویه
- محاسبه مساحت مثلث قائم‌الزاویه با استفاده از روابط مثلثاتی
محاسبه مساحت مثلث قائم‌الزاویه با فرمول اصلی
برای محاسبه مساحت مثلث قائم‌الزاویه با فرمول اصلی، به اندازه قاعده و ارتفاع آن نیاز داریم. همان‌طور که بالاتر گفتیم، با ضرب قاعده و ارتفاع در یکدیگر و تقسیم آن بر ۲، می‌توان مساحت مثلث قائم‌الزاویه را حساب کرد:
مثال: اندازه ارتفاع و قاعده یک مثلث قائم‌الزاویه به ترتیب ۶ و ۴ سانتی‌متر است، مساحت این مثلث چقدر می‌شود؟
جواب: وقتی قاعده و ارتفاع مثلث را داشته باشیم، راحت‌ترین کار استفاده از فرمول اصلی مساحت مثلث است:
A= (h × b ) ÷ ۲
A= (۶ × ۴ ) ÷ ۲
۳/۵ =۲ ÷ A= ۲۴
مساحت مثلث قائم الزاویه با وتر
اگر اندازه قاعده یا ارتفاع مثلث قائم‌الزاویه مجهول باشد، به کمک قضیه فیثاغورس می‌توانیم آن را محاسبه کنیم و سپس مساحت مثلث را در بیاوریم. طبق قاعده فیثاغورس:
c² = a² + b²
- c: وتر مثلث قائم‌الزاویه
- a و b: قاعده و ارتفاع مثلث قائم‌الزاویه
پس اگر اندازه وتر و یکی از ضلع‌های مجاور زاویه قائمه را داشته باشیم، مساحت ضلع دیگر قابل محاسبه است. این مسئله را در ادامه با یک مثال توضیح می‌دهیم:
مثال: اندازه وتر و قاعده در یک مثلث قائم‌الزاویه به ترتیب ۱۰ و ۶ سانتی‌متر است. باتوجه به این اطلاعات، مساحت مثلث را حساب کنید.جواب: ابتدا به کمک قضیه فیثاغورس اندازه ارتفاع مثلث را محاسبه می‌کنیم:
c²= a² + b²
۱۰²= ۶² + b²
۱۰۰= ۳۶ + b²
۱۰۰ – ۳۶ = b²
۶۴ = b²
b = √۶۴ = ۸
:حالا که مقدار ضلع دیگر مثلث (ارتفاع) را به دست آوردیم، از طریق فرمول اصلی مساحت مثلث جواب را پیدا می‌کنیم
A= (h × b ) ÷ ۲
A= (۸ × ۶ ) ÷ ۲
۲۴ = A= ۴۸ ÷ ۲
فرمول هرون برای محاسبه مساحت مثلث قائم الزاویه
فرمول هرون برای محاسبه مساحت انواع مثلث‌ها کاربرد دارد. از این فرمول زمانی استفاده می‌کنیم که اندازه قاعده، ارتفاع و وتر مثلث قائم‌الزاویه را داشته باشیم. فرمول هرون به این صورت نوشته می‌شود:
(A= √ (s (s -a) × (s-b) × (s-c)
2 ÷ s=(a+b+c)
- s: محیط مثلث تقسیم بر ۲
- a، b و c: اندازه قاعده، ارتفاع و وتر (۳ ضلع) مثلث
مثال: اگر اندازه قاعده، ارتفاع و وتر یک مثلث قائم‌الزاویه به ترتیب ۶، ۸ و ۱۰ سانتی‌متر باشد، مساحت آن را با فرمول هرون حساب کنید:جواب: چون اندازه ۳ ضلع مثلث را داریم، از فرمول هرون استفاده کنیم. ابتدا مقدار S (نصف محیط مثلث) را حساب می‌کنیم:
۲ ÷ s=(a+b+c)
۱۲= ۲ ÷ ۲۴ = ۲ ÷ s=(۶+۸+۱۰)
حالا مقدار به دست آمده را در فرمول هرون می‌گذاریم و مساحت مثلث قائم‌الزاویه را حساب می‌کنیم:
محاسبه مساحت مثلث قائم الزاویه با ۲ ضلع و زاویه بین آن‌ها
اگر اندازه قاعده و وتر یا ارتفاع و وتر مثلث قائم‌الزاویه و زاویه بین آن‌ها را داشته باشیم، می‌توانیم به کمک فرمول زیر، مساحت آن را حساب کنیم:
A= ۱ ÷ ۲(a×b) × sinC
در فرمول بالا، a و b نماد ۲ ضلع مجاور یکدیگرند و سینوس C نماد زاویه بین آن‌هاست.
مثال: اندازه وتر و ارتفاع یک مثلث قائم‌الزاویه ۱۰ و ۷ سانتی‌متر و زاویه بین آن‌ها ۵۰ درجه است. مساحت این مثلث را حساب کنید:جواب: چون اندازه ۲ ضلع و زاویه بین آن‌ها را داریم، می‌توانیم از طریق فرمول ۲ ضلع و زاویه بین آن‌ها مساحت مثلث قائم‌الزاویه را حساب کنیم:
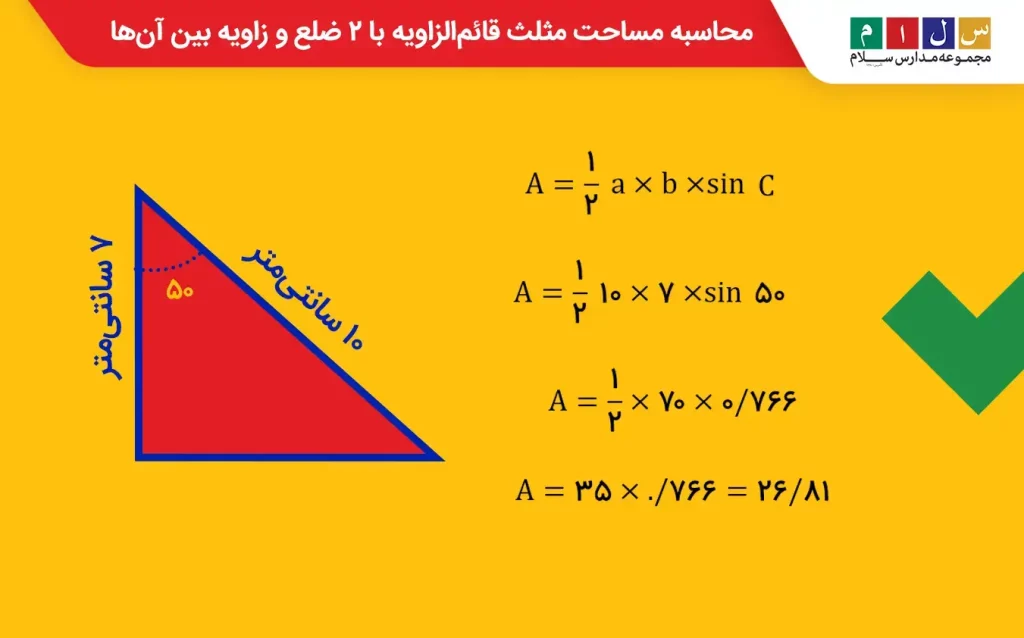
A=(۱ ÷ ۲ ) ( a × b) × sinC
A=(۱ ÷ ۲ ) ( ۱۰ × ۷ ) × sin۵۰
A=(۱ ÷ ۲ )(۷۰) × ۰/۷۶۶
۲۱/۸۶ =A= ۳۵ × ۰/۷۶۶
مثال برای محاسبه مساحت مثلث قائم الزاویه
حالت‌ها و روش‌های مختلف محاسبه مساحت مثلث قائم‌الزاویه را با یکدیگر بررسی کردیم. حالا بیایید برای تکمیل و یادگیری عمیق این مبحث، چند مثال کاربردی با هم حل کنیم.
مثال اول: محاسبه مساحت مثلث قائم الزاویه متساوی الساقین
یک استخر به شکل مثلث قائم‌الزاویه داریم که ساق‌های آن با هم برابرند. اگر ارتفاع این مثلث ۵ سانتی‌متر باشد، مساحت آن را حساب کنید:جواب: این سوال یک نکته انحرافی دارد: در مثلثهای قائم‌الزاویه متساوی‌الساقین، ارتفاع و قاعده مثلث با یکدیگر برابرند. اگر ارتفاع یک مثلث ۵ سانتی‌متر باشد، پس حتما قاعده آن هم همین مقدار است. حالا که قاعده و ارتفاع مثلث را داریم، از طریق فرمول اصلی مساحت مثلث، جواب را به دست می‌آوریم:
A= (h × b ) ÷ ۲
A= (۵ × ۵ ) ÷ ۲
۳/۵ =۲ ÷ A= ۲۴
مثال دوم: محاسبه ضلع مثلث قائم الزاویه از روی مساحت آن
مساحت یک مثلث قائم‌الزاویه ۲۰ و قاعده آن ۴ سانتی‌متر است. ارتفاع این مثلث را محاسبه کنید:جواب: وقتی مساحت و اندازه قاعده یا ارتفاع مثلث را داشته باشیم، با جای‌گذاری آن‌ها در فرمول مساحت مثلث می‌توانیم اندازه ضلع دیگر را حساب کنیم:
A= (h × b ) ÷ ۲
۲ ÷ (h ×4) =۲۰
۱۰ = h= (۲۰ × ۲ ) ÷ ۴
مثال سوم: محاسبه مساحت مثلث قائم الزاویه با وتر
بزرگ‌ترین ضلع یک مثلث قائم‌الزاویه ۱۲ سانتی‌متر و ارتفاع آن ۱۰ سانتی‌متر است. مساحت این مثلث چند سانتی‌متر است؟جواب: وقتی مقدار وتر و یکی از ضلع‌های مجاور زاویه ۹۰ درجه را در مثلث قائم‌الزاویه داشته باشیم، می‌توانیم به کمک قضیه فیثاغورس، ضلع بعدی را هم حساب و مساحت مثلث را پیدا کنیم:
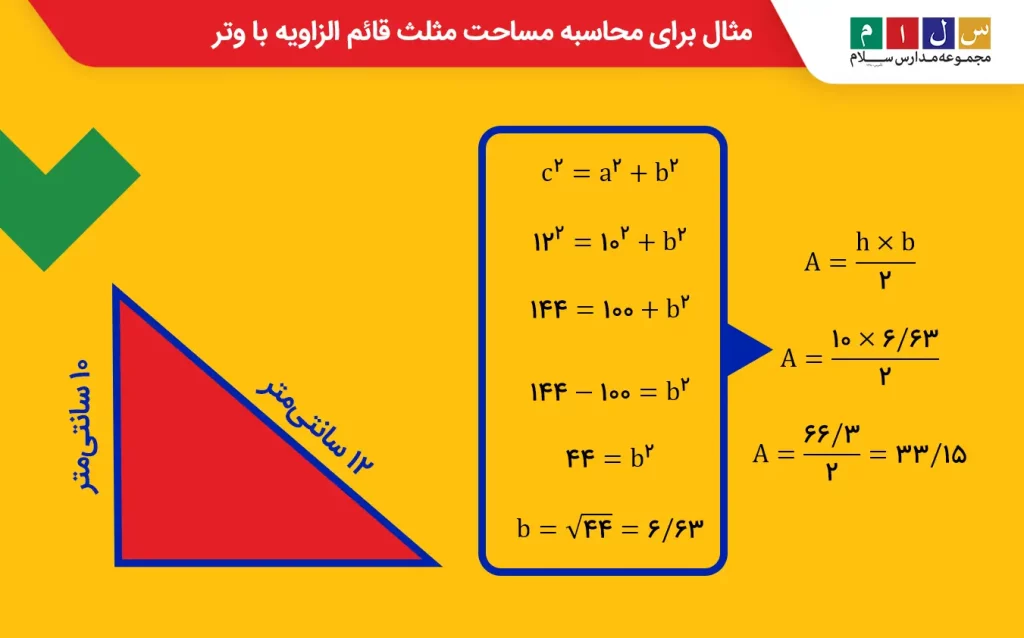
حالا که اندازه قاعده مثلث را به دست آوردیم، می‌توانیم با استفاده از فرمول اصلی مساحت مثلث، جواب سوال را حساب کنیم:
A= (h × b ) ÷ ۲
A= (۱۰ × ۶/۶۳ ) ÷ ۲
۳۳/۱۴=A= (۶۶/۳ ) ÷ ۲
سخن پایانی
۲ ضلع مجاور زاویه۹۰درجه در مثلثهای قائم‌الزاویه، قاعده و ارتفاع یکدیگرند و ضلع مقابل زاویه قائمه، وتر است. مساحت مثلث قائم‌الزاویه از طریق فرمول اصلی مساحت مثلث، یعنی «قاعده ضربدر ارتفاع تقسیم بر دو (۲A = h × b ÷ ) محاسبه می‌شود. البته برای محاسبه مساحت مثلث از فرمول‌های دیگری مانند فرمول هرون، قاعده فیثاغورس و روابط مثلثاتی هم می‌توان استفاده کرد. یک نکته دیگر هم در این مقاله یاد گرفتیم: در مثلثهای قائم‌الزاویه متساوی‌الساقین، قاعده و ارتفاع با یکدیگر مساوی‌اند و داشتن یکی از آن‌ها برای محاسبه مساحت مثلث کافی‌ست. امیدواریم که مطالعه این مقاله در یادگیری عمیق و کامل این مبحث کمکتان کرده باشد.
